Vance at Six Figure Investing wrote an excellent post about VIX1D - I am upset that he beat me to it, and wrote a comprehensive and thorough post; take a look.
Volatility Futures & Options
Weekly market report
Weekly market update: volatility indexes and futures
This week's market movements were largely driven by renewed recession fears in the wake of a sharp rise in office vacancies and other signs of economic slowdown. Volatility indexes were mixed: the benchmark Canadian volatility index based on S&P TSX 60 rose by 1.87 points to 15.52, and VTA35 - benchmark volatility index for Israel fell by -2.67 points to 16.87 - maybe Passover effect?
As usual I publish 50% confidence ranges for SPX and other indexes. These ranges are based on empirical distribution, and are very different from those implied by normal distribution ( 1std/68%, etc )
Over the last week VIX futures curve rotated - a typical "tilt" movement with front months falling, and back months rising.
For the next week my model predicts VIX futures to trade slightly lower.
I am still working on incorporating seasonality into the model (nov,dec futures), better formatting for the table, and also something to recommend specific calendar spread trades - not only by the expected change, but also by risk.| Expiration Date | Settle | Total Volume | forecast | change |
|---|---|---|---|---|
| 2023-04-19 | 19.98 | 62532 | 19.8 | -0.17 |
| 2023-04-26 | 21.12 | 0 | 20.25 | -0.87 |
| 2023-05-03 | 20.35 | 0 | 20.65 | 0.3 |
| 2023-05-10 | 20.8 | 0 | 21.02 | 0.22 |
| 2023-05-17 | 21.5 | 46173 | 21.35 | -0.15 |
| 2023-06-21 | 22.74 | 12118 | 22.57 | -0.18 |
| 2023-07-19 | 23.55 | 5422 | 23.17 | -0.38 |
| 2023-08-16 | 23.81 | 3957 | 23.58 | -0.23 |
| 2023-09-20 | 24.29 | 2908 | 23.9 | -0.39 |
| 2023-10-18 | 24.4 | 1342 | 24.06 | -0.34 |
| 2023-11-15 | 24.3 | 560 | 24.17 | -0.13 |
| 2023-12-20 | 23.95 | 126 | 24.27 | 0.32 |
VIX futures spreads
A short post on practical pricing VIX futures curve with application to trading futures spreads. Here is the VIX futures curve based on Friday's (latest at the time of writing) settlement price, and prices from 1 week ago. Market up, VIX futures down, some aberrant settlement values in November that we should not focus on.
The raw prices from futures are difficult to work with, so the term structure is converted to a functional space - that is we find a function that can represent all kinds of futures curves. There is no "simple regression" approach that can work for raw prices as futures time to maturity changes from minute to minute, but in a functional space that is possible. The solid lines in the chart above are not simple connections between the dots - they are the theoretical values of the futures curve, the functional projection I wrote about.
In this functional form we can create forecasting models that predict how the term structure will evolve from one time period to the next.
The uncertainly in the forecasting model can be projected back into the price space, and the resulting confidence intervals have financially intuitive properties - they are not symmetric around the forecast, and confidence intervals have their own term structure: wider near expiration, and narrower for back months.
If they moved in parallel, then predicted prices would like on the 45 degree line ( in grey dashes ) . Also there is skew although the chart does not show it well.
How will my forecasts turn out? We'll find out next week.
If you are interested in my work - I am looking for a full time job, or a consulting opportunity, and my email is on the right-side bar.
Weekly market update
This week saw some positive movement in the stock market, with the S&P 500 rising by 3.48% and the Dow Industrials rising as bank concerns ebbed. The STOXX 50 also rose by 4.46%, while the VIX and VSTOXX fell by -3.04 points and -5.46 points respectively. In fact, VSTOXX was the biggest loser among international volatility indexes that I am tracking.
Asian markets also experienced positive growth, with the Nikkei 225 rising by 2.40% and the VNKY falling by -2.42 points. As usual here are the confidence ranges for next week.
An excellent weekend read from Eric Falkenstein titled "FTX's Mythical Origin Story" Check it out!
DVOL Futures, first day of trading
Few weeks ago I published a post on pricing DVOL futures. Today is their first day of trading on Deribit, and we can draw some conclusions.
1 - The term structure is really flat
a single future was listed with month to expiration and spot @ 63.34 future @ 63.40 this is far flatter than what I would expected. The charts that I posted would have the 1-month future trading at least 3-5 points higher than the index.
2 - Market makers are point-wide in size.
In the oderbook you can see someone is 1 point wide, 1000 up, but small sizes are quoted quite tightly.
3 - Trading in small size is brisk. The launch looks like a success.
Congratulations, Deribit! We will be watching the contract very closely!
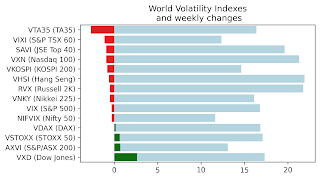
Weekly market report
Wall st delivered a mixed bag of news with VIX, VNKY, and VSTOXX and their underlying markets almost unchanged. VXD - volatility index based...
-
As I am sure all of you know Russia has began a full scale war against my home country Ukraine. Please make no mistake - Putin's goal ...
-
Yesterday I found another piece of ignorance on Medium: Stop Watching The VIX, Just Make Your Own tl;dr : Just use ATM straddles 🤦 This is...
-
The biggest news this week is that Deribit is moving ahead with launching futures on their DVOL Bitcoin volatility index. Like with every ne...











