TVIX Vol & Applets

One of the blog readers emailed me the following question: [What is the] amount of vol in every 10k shares of tvix. Is it possible to break it down to spx terms (straddles) or what you are buying along the curve?


I answered as follows: There is no simple answer ... but I'll try to provide so rules of thumb without a formal model . To compare TVIX with SPX straddle, let's consider the simplest case where straddle has 30 days to
expiration, so the same maturity as VIX. VXX , which holds VIX futures interpolated to 30 day maturity will have about 0.5 β to the VIX, and TVIX will have β about 1 (that is actually when I get from regression) . [Edit: to clarity VIX has maturity of SPX + 30 and beta ≈ 1, VXX SPX + 60 and beta ≈ 0.5]

Since ATM straddle is approximately linear in vol, % change for 30-day ATM straddle would be about the same as % change in the TVIX. This is of course a "local" relationship. As the straddle moves around it will no longer be ATM and will lose or gain Γ, so the relationship will change.

To generalize this to any maturity you would have to figure out how vols move. Again, without having a formal model the rule of thumb is that vol changes are inversely proportional to sqrt(T). So if 1 month straddle has β = 1, 4 month straddle will have β = 0.5, and half-month straddle will have β of about 1.4.


About 2 years ago I published few posts (1,2,3) about VIX future movements, and used few applets for interactive illustrations. These applets use Adobe Shockwave, and do not work on all browsers. I created them using a product called Xcelcius that was taken over by SAP and as far as I know has been deprecated. Can any of the readers suggest a way for me to create interactive applets to demonstrate non-linear features of VIX products, something simple that would not require significant programming?

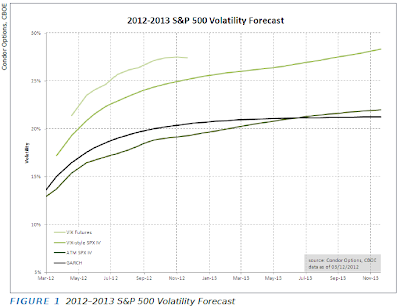
Volatility Forecasts

The chart above was taken from March issue of Expiring Monthly magazine (with author's permission, of course) . The article titled "2012 Volatility Forecasts for the S&P 500" Jared Woodard writes about structural differences between the products. I wanted to try more mathematical view, however I did not make significant progress in explaining the difference. Below are some thoughts and ideas I came up with.

Ignoring GARCH which is a statistical model we have 3 different expected volatility curves: ATM Implied vols, VIX-style vol, and VIX futures. The interesting thing is that all three are quite different mathematically. If we gloss over some technicalities I figured as follows:

let r be the return of underlying index from time 0 (today) to T (expiration). Lowercase t is 30 days before T and denotes VIX expiration date. Subscripts have been added for clarification.

ATM IV (Black-Scholes ATM Straddle IV) is proportional to the straddle price. The ratio between ATM IV and VIX-style IV is 1 if distribution is Normal. Using few simulations, and few limited formulas I hypothesize that the ratio is < 1 for leptokurtic distributions (excess kurtosis will influence r^2 faster than |r|), but I was not able to prove it mathematically. Since market returns have excess kurtosis it should not be surprising to see VIX-style IV to be always higher than ATM IV.

Explaining VIX futures is trickier - the term under the square root is forward volatility from VIX expiration to SPX expiration, and is not the same as two volatilities above. I could not figure out how to make a direct connection to the volatilities above, but will note that VIX futures price is <= to the square root of forward variance, which can be calculated from VIX-style IVs, see Tale of Two Indexes, formula 11.