I recently came across an old article titled Reliability of the Maximum Drawdown, and suggest that trades familiarize themselves with the ideas mentioned there. I would like to suggest an idea that may be a way forward.
The mathematics of maximum drawdown (expected maximum drawdown, and its distribution) are far from trivial, and many other related measures (for example expected length of drawdown) afaik have not been seriously studied at all.
The problem with max-measures, like mentioned in the article above, is that they are extreme measures, and thus are at the very corner of distribution charts. If you have a strategy that suffered a maximum drawdown of x% you know that such drawdown is possible, but if you observe another strategy with smaller drawdown, you can hardly be sure that it will not suffer from a greater drawdown in the future.
One possible way forward is to use "average measures" - average drawdown and average drawdown length instead of their max counterparts. Intuition suggests (and my extensive monte carlo confirms) that these measures have smaller variability, smaller skewness, and more predictive (as measured by linear and nonlinear correlations) from one period to the next. These measures seem to scale linearly with time, with the scale coeffcient depending on kurtosis. I don't have the maths to take this much further on my own, but if you have some ideas please leave a comment or send me an email.
Subscribe to:
Post Comments (Atom)
Weekly market report
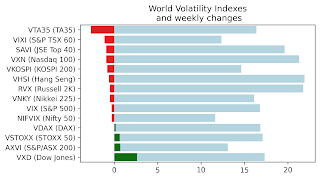
Wall st delivered a mixed bag of news with VIX, VNKY, and VSTOXX and their underlying markets almost unchanged. VXD - volatility index based...
-
John “Hojun” Hwang is the author of VIX, VIX Futures, and VIX ETNs, a conceptual guide to trading the VIX index. He graduated with degrees i...
-
This week 's market movements were largely driven by renewed recession fears in the wake of a sharp rise in office v...
-
Wall st delivered a mixed bag of news with VIX, VNKY, and VSTOXX and their underlying markets almost unchanged. VXD - volatility index based...


No comments:
Post a Comment