Define cdf and pdf as:
Then moments of x are:
Source: Modeling and Generating Daily Changes in Market Variables Using A Multivariate Mixture of Normal Distributions. My special thanks to Dr. Jin Wang for his correction to the skew formula.
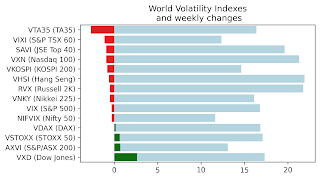
Wall st delivered a mixed bag of news with VIX, VNKY, and VSTOXX and their underlying markets almost unchanged. VXD - volatility index based...
No comments:
Post a Comment