When I'm wrong, I must admit that I'm wrong. Some time ago I published a post pointing out potential vulnerability of VIX settlement price to manipulation. As was recently pointed by a reader (and I contacted CBOE to confirm the details) I was incorrect in my understanding of settlement calculation of VIX index.
The reader pointed out that "bidding 0.05 for a 1 lot makes the option very unlikely to be included in the strip. Indeed, if you have a significant size of seller at 0.05, your bid will be hit and filled while no other bid would be left behind which would make the option a "0 bid" option, hence non included in the official strip.
You would be left like many traders before you wondering how they got filled on their bid thru the official rotation while this strike isn't included in the official strip."
CBOE documents state that the settlement price is calculated from all opening trades, and opening quotes for strikes where trades were not available. My initial understanding was that that zero bid filter applied only to regular everyday VIX calculation that is calculated from quotes, but not to settlement calculation that is based on trades. However the correct understanding that zero bid filter applies to settlement calculation as well. So e.g. in the case of some really low put strike, if you submit a nickel bid at the pre-open, it will get filled, but if the resulting opening quote has zero bid that strike will be ignored in the VIX settlement calculation.
My sincere apologies to all the readers, and thanks to WB for pointing out the error.
Nations VolDex (VOLI)
Nations VolDex is an alternative market volatility index. As everyone knows VIX product suite is a huge success and a big revenue generator for CBOE, which holds exclusive rights to the product. ISE has teamed up with Chicago-based NationsShares to launch VIX-like product and hopefully bring over some of that revenue to ISE.
How is VolDex different? VolDex is calculated from ATM options on SPY, while VIX is calculated from all options on SPX. Exact algorithm for VolDex is currently not disclosed (yes, I emailed and called the company). The basic overview can be found in SEC filing from ISE, but the document does not describe eactly how they calculate IV.
As one can plainly see the two indexes are not very different, the levels are quite correlated. VIX tends to run higher than VolDex.
The ratio (VIX/VolDex) is pretty much constant through the time, with average of 1.094 and median of 1.096, showing no significant skew.
The ratio does not appear to be related to the level, but difference (VIX-VolDex) shows linear relation to the VIX level. This (admittedly very simple) analysis leads me to suggest the simplest possible model: VolDex = 0.92 * VIX + noise. Of course, a more complicated model would be advised for trading, but this basic model has in-sample R^2 of 0.99.
Before I present my own analysis here are two articles from Risk, first introducing the VolDex, and second from CBOE providing a response on technical points, as well as CBOE's comment letter to SEC.
Vix challenged by new volatility index, by Yakob Peterseil (try this link, or this)
CBOE responds on Vix, by John Hiatt (link)
CBOE's comment letter to SEC (link)
In the Risk article Scott Nations is quoted saying "Because the spot Vix is impossible for traders to replicate, it becomes impossible for arbitrageurs to keep the levels of Vix futures consistent with the spot level of the Vix" I don't see that as valid argument, as I don't see how one can statically replicate VolDex futures. (Dynamic replication is possible, and I suspect it will be a practical nightmare)
CBOE argues (in the SEC comment) that VolDex is not a broad-based index, and can be easily manipulated. They provide an example that on the futures expiration day index will be calculated using only two front month SPY, and depending on where the spot is to the strike, most of the index value can come from a single option. I believe that the argument is theoretically valid, but I am having a difficulty figuring out how much the index could be manipulated in such way. If you have any thoughts on how to quantify this effect, send me an email.
On the other hand it is possible that the index would be more robust to manipulation: it does not use far otm puts that have disproportionate weight in the VIX. I wrote about this earlier in How to manipulate VIX settlement price. ATM options are most deep and liquid of any series, so manipulating them would be very expensive.
Overall, I think that both CBOE and ISE/Nations know that the indexes are not that much different from each other, and the arguments presented are of limited practical relevance. ISE also know that if they were to launch some volatility index that is really really different than VIX it will likely fail to attract any liquidity. I think the goal here is that VolDex will be similar enough to VIX that cross-hedging is possible, plus ISE will likely to provide substantial discounts on fees for the new product to attract market-makers.
At the time of writing VolDex options are pending SEC approval, and there is no mention of VolDex futures at all.
How is VolDex different? VolDex is calculated from ATM options on SPY, while VIX is calculated from all options on SPX. Exact algorithm for VolDex is currently not disclosed (yes, I emailed and called the company). The basic overview can be found in SEC filing from ISE, but the document does not describe eactly how they calculate IV.
As one can plainly see the two indexes are not very different, the levels are quite correlated. VIX tends to run higher than VolDex.
The ratio (VIX/VolDex) is pretty much constant through the time, with average of 1.094 and median of 1.096, showing no significant skew.
Before I present my own analysis here are two articles from Risk, first introducing the VolDex, and second from CBOE providing a response on technical points, as well as CBOE's comment letter to SEC.
Vix challenged by new volatility index, by Yakob Peterseil (try this link, or this)
CBOE responds on Vix, by John Hiatt (link)
CBOE's comment letter to SEC (link)
In the Risk article Scott Nations is quoted saying "Because the spot Vix is impossible for traders to replicate, it becomes impossible for arbitrageurs to keep the levels of Vix futures consistent with the spot level of the Vix" I don't see that as valid argument, as I don't see how one can statically replicate VolDex futures. (Dynamic replication is possible, and I suspect it will be a practical nightmare)
CBOE argues (in the SEC comment) that VolDex is not a broad-based index, and can be easily manipulated. They provide an example that on the futures expiration day index will be calculated using only two front month SPY, and depending on where the spot is to the strike, most of the index value can come from a single option. I believe that the argument is theoretically valid, but I am having a difficulty figuring out how much the index could be manipulated in such way. If you have any thoughts on how to quantify this effect, send me an email.
On the other hand it is possible that the index would be more robust to manipulation: it does not use far otm puts that have disproportionate weight in the VIX. I wrote about this earlier in How to manipulate VIX settlement price. ATM options are most deep and liquid of any series, so manipulating them would be very expensive.
Overall, I think that both CBOE and ISE/Nations know that the indexes are not that much different from each other, and the arguments presented are of limited practical relevance. ISE also know that if they were to launch some volatility index that is really really different than VIX it will likely fail to attract any liquidity. I think the goal here is that VolDex will be similar enough to VIX that cross-hedging is possible, plus ISE will likely to provide substantial discounts on fees for the new product to attract market-makers.
At the time of writing VolDex options are pending SEC approval, and there is no mention of VolDex futures at all.
F# In Finance & Big Data In Finance

Two excellent events Andrew Sheppard of Fountainhead (and HPC & GPU Supercomputing Meetup)
F# in Finance (London)
If you are a functional programmer (even in a language other than F#, such as Haskell, Scala, Clojure, Ocaml, Erlang); or a quant, trader, risk officer, Big Data programmer, Data Scientist, software development manager, or anyone who wants to get more done -- and done better -- with less code:
- Come and see how F# is being used in finance for Machine Learning, Parallel Programming, Big Data and the Cloud. Plenty of lessons at this event for programmers in other functional languages.
- The event is also hosting a recruitment fair for functional programmers. Whether you are looking for functional programming talent, or looking to break into functional programming as a career move, this event is the place to be.
- Meet Don Syme, inventor of F#!
The second event is Big Data In Finance MOOC. There are two tracks - no cost open access, and a paid professional access which provides deeper learning experience and also a certificate from Baruch college. Several practical projects are covered: CVA (credit valuation adjustment) which Dr Sheppard has extensive experience, Data Mining & Machine Learning using Hadoop, and Building a Look-Ahead (Predictive) Ticker Plant.
ASX To Expand The Range of Volatility Products
More exciting news for Australia-based volatility traders: in a recent article in Risk Brian Goodman, product development manager at ASX was quoted that ASX is looking to expand the range of ASX Vix futures-linked instruments to include exchange-traded funds and structured products.
This is certainly a smart move - at this point liquidity in Asian volatility products is low. The plan is that launching a "packaged" retail-friendly ETF product will attract interest from wider group of traders.
Original link.
This is certainly a smart move - at this point liquidity in Asian volatility products is low. The plan is that launching a "packaged" retail-friendly ETF product will attract interest from wider group of traders.
Original link.
ASX VIX Futures Launched
ASX finally launched futures on its volatility index. As I understand the futures were listed yesterday (Monday) but there were no trades. Today (Tuesday) 1 contract traded. Not a great start, but you have to start somewhere ....
I am having a hard time accessing data for the contract. On Bloomberg, the index is SPAVIX <INDEX> , but the ticker for the futures is AS51VIX <INDEX> . I tried checking the prices just few minutes ago, but there was no data for any of the futures contracts, as if they don't exist. Edit: the current contract is VIA <INDEX> .
Exchange's own website is not much of a help either - futures summary table does not have the data for the VIX contract (futures root VI). I was able to figure out this non-linked page with the data:
The volume in other international volatility contracts on Tuesday was:
RTSVX (Russian volatility index) - 2 contracts
VHSI (Hong-Kong volatility index) - 19 contracts
VNKY (Nikkei volatility index) - 71 contracts
I am having a hard time accessing data for the contract. On Bloomberg, the index is SPAVIX <INDEX> , but the ticker for the futures is AS51VIX <INDEX> . I tried checking the prices just few minutes ago, but there was no data for any of the futures contracts, as if they don't exist. Edit: the current contract is VIA <INDEX> .
Exchange's own website is not much of a help either - futures summary table does not have the data for the VIX contract (futures root VI). I was able to figure out this non-linked page with the data:
| Expiry | Last | Bid | Ask | Volume |
|---|---|---|---|---|
| Spot | 12.295 | |||
| Nov 13 | 12.45 | 13.10 | 0 | |
| Dec 13 | 12.00 | 11.90 | 12.10 | 1 |
The volume in other international volatility contracts on Tuesday was:
RTSVX (Russian volatility index) - 2 contracts
VHSI (Hong-Kong volatility index) - 19 contracts
VNKY (Nikkei volatility index) - 71 contracts
Two pretty good articles on HFT
These articles Jacob Loveless were posted few months ago on ACM (Association for Computing Machinery) blog, but I just came across them.
Barbarians at the Gateways includes details on specific HTF trading strategy
Online Algorithms in High-frequency Trading provides high-level overview of some mathematics that is used for data analysis
Barbarians at the Gateways includes details on specific HTF trading strategy
Online Algorithms in High-frequency Trading provides high-level overview of some mathematics that is used for data analysis
Reading Up on Electronic Trading
I was reading Nerds on Wall Street, and came across the following paragraph:
Update: finished reading Whitcomb's book. No content that I found useful.
David Whitcomb, a market microstructure economist at Rutgers University and coauthor of a 1988 book on electronic trading strategies faced ... skepticism selling his ideas to Wall Street. Finding no institutional backing, he joined forces with a computer scientist colleague to found Automated Trading Desk (ATD) in the proverbial garage in Charleston, SC. The firm reportedly grew from its first trade in 1990 to one of the leading electronic market participants, trading on average more than 200 million shares daily, or 6 percent of the volume on both the NYSE and NASDAQ.Which got me interested in the Whitcomb's book. The work in reference - Transaction Costs And Institutional Investor Trading Strategies - proved to be quite difficult to find. It is not available for purchase anymore, and I could not find a local public library that carries the title. Thankfully a local university had one in their collection, and girlfriend borrowed a copy for me yesterday. Will keep you updated!
Update: finished reading Whitcomb's book. No content that I found useful.
DTN.IQ / IQFeed Caveat Emptor
I started working on a new strategy about a month ago and needed a cheap source of historical data for testing. DTN.IQ seem to fit the bill and budget, until yesterday I discovered that historical quotes data set that DTN.IQ provides foes not include all quotes, but only quotes at the time of a trade. For example, you have an illiquid stock that does not trade frequently.
made-up example
time,bid,ask,last
12:03:00,55.01,55.07,55.01 <- reported by the feed
12:04:00,55.02,55.08 <-no trade, not reported by the feed
12:05:00,55.05,55.16 <-no trade, not reported by the feed
12:06:00,55.05,55.16,55.10 <- reported by the feed
Even though quotes may be updating in between the trades, DTN.IQ does not provide that data.
Otherwise, my experience with the service has been satisfactory, and I will continue using the product for testing live data and historical data.
made-up example
time,bid,ask,last
12:03:00,55.01,55.07,55.01 <- reported by the feed
12:04:00,55.02,55.08 <-no trade, not reported by the feed
12:05:00,55.05,55.16 <-no trade, not reported by the feed
12:06:00,55.05,55.16,55.10 <- reported by the feed
Even though quotes may be updating in between the trades, DTN.IQ does not provide that data.
Otherwise, my experience with the service has been satisfactory, and I will continue using the product for testing live data and historical data.
What's going on with this blog
As you know I have not posted in a while. My current trading does not involve options, or any volatility-related instruments, and it became harder to come up with quality material. At the beginning of June I started trading, and had no time to follow volatility research. As of right now I will either update this blog less frequently with volatility-related news or expand coverage to include statistical arbitrage and machine learning. Good luck trading, and hedge your deltas!
VHSI Update and Forecast
VHSI May futures expired on 30th, last week. Unfortunately I was/am very busy with launching a new strategy into production and could not update the blog on time. Also somehow I missed the futures settlement value so I am using index settlement value instead in the Volatility Forecasts Tracker spreadsheet. Over May results were good, with my model providing better forecasts than the market and almost making up for the losses in April. Charts have been updated with the latest numbers.
My forecast for next expiration is for 16.29 vs futures value 17.25 (Monday settlement value).
My forecast for next expiration is for 16.29 vs futures value 17.25 (Monday settlement value).
VIX, VSTOXX June 2013 Forecasts
Yesterday all CBOE and Eurex volatility indexes settled - so forecasting results are in, and as always all the forecasts and results are logged in the Volatility Forecasts spreadsheet . The signals were all correct except for GVZ - Gold Volatility Index, which rallied on gold's quite unexpected decline.
The technical issues with data solved, and I have forecasts for all CBOE indexes.The forecasts are as follows:
VIX 13.47 vs 15.30 in the market
VSTOXX 17.50 vs 19.55
GVZ 23.63 vs 23.65 <- only 0.02 difference between market and forecast
VXEEM 18.77 vs 20.05
VXEWZ 19.39 vs 21.80
OVX 22.48 vs 24.75
VXN 14.55 vs 16.25
The technical issues with data solved, and I have forecasts for all CBOE indexes.The forecasts are as follows:
VIX 13.47 vs 15.30 in the market
VSTOXX 17.50 vs 19.55
GVZ 23.63 vs 23.65 <- only 0.02 difference between market and forecast
VXEEM 18.77 vs 20.05
VXEWZ 19.39 vs 21.80
OVX 22.48 vs 24.75
VXN 14.55 vs 16.25
MATLAB Computational Finance Conference, Options data for your iPhone
A friend just forwarded me the link - MATLAB Computational Finance Conference will take place in two days on Thursday at Marriott Marquis. Paul Willmott and Attilio Meucci are among the speakers, and the presentations side I hope to hear about matlab tools for machine learning and for dealing with big data and big compute issues. If you're going and want to meet up, send me an email!
iVerit Option Chain is an application that delivers delayed (free) or real-time ($24.99) options data for your iPhone. If you need to leave your desk but can't tear away from that desk terminal - now you can!
iVerit Option Chain is an application that delivers delayed (free) or real-time ($24.99) options data for your iPhone. If you need to leave your desk but can't tear away from that desk terminal - now you can!
VNKY Forecast
May futures tied to Nikkei Volatility Index expired today, settling at 26.65, slightly higher than futures level month ago, and higher than my forecast. June futures closed at 25.45 and my forecast is for the index to settle at 24.58. Despite increase in the volatility levels, VNKY did not break 30 barrier, and slight decline that the model suggests seems reasonable. Will resume regular blogging toward the end of May.
RTSVX June Forecast
Sorry I have been really busy lately and don't have a lot of free time to provide updates. However one things that keeps me on schedule are futures forecasts that I publish for all available volatility futures in the world. Today futures on Russian VIX - RTSVX index settled at 19.82, closer to my forecast and correct on direction. Front month futures - expiring on the 7th of June 2013 are trading at 22.40, while my model suggests that the index will likely settle around 19.67. As usual all forecasts are available on Volatility Tracker page.
VHSI May Forecast
Contracts tied to volatility of Hong-Kong benchmark HSI index expired today, settling at 15.28, lower than the futures level a month ago, and closer to my forecast of 14.82. For the next expiration I forecast VHSI index to settle at 15.67 vs futures level of 17.85. It seems that the spike in VIX we experienced about two weeks ago in the was just that - a temporary specific (VHSI did not experience a parallel move) spike, and not a return to a higher volatility levels. As usual all forecasts are recorded on Forecasts Tracker spreadsheet.
Expiring Monthly
I just found out over the weekend: the editors of Expiring Monthly apparently made two back issues available for free download: July 2011 and September 2011. Enjoy!
Visual Quantitative Finance: Interview with Michael Lovelady
Q: Please tell us about your background.
A: My early educational background was in math and psychology. I think in most of what I have done since, I keep going back to those fields in some way. Starting in the late 1980s, I worked as a consulting pension actuary for Towers Watson and later for Price Waterhouse. In 1998, I started a small hedge fund with an emphasis on emerging technology. After the 2000-2002 collapse, my focus expanded to include volatility reducing strategies. In particular, blending traditional portfolio management with quantitative overlays. One of the ideas involves a hybrid options structure I call a synthetic annuity or SynA.
Q: Straight to the topic: tell us about your new book.
A: Visual Quantitative Finance
The books are related but are also meant to be standalone in scope. Profiting with Synthetic Annuities was written to propose a middle ground between modern portfolio theory and related mean-variance portfolios— which are great at capturing risk premiums over the long term but lack a risk discipline— and quantitative strategies that have great risk disciplines but are not so good at capturing risk premiums. The question is whether it is possible to bridge the gap and at what cost?
In that book, I laid out a “visual architecture” for options-based structured securities and used it to illustrate synthetic annuities structure and measure their risk/return characteristics. For the most part, the book is a practical how-to explanation for setting up options-based positions and managing them to achieve higher yields, but doing it within the constraints of risk budgets. Because I wanted to speak to institutional trustees and others who might not have a strong technical slant, I intentionally stayed away from the underlying math. So, I used a lot of graphics to communicate the ideas.
In this book, Visual Quantitative Finance
Q: Can you describe the basis of the visual method?
A: Sure, here is a figure from the book. It shows the basic framework for the visual method. It is an Excel spreadsheet with 95 Rows and seven columns. The first two columns are just a discrete approximation to the standard normal distribution. The next four columns show the stock return, the stock price, the call option payoff and the weighted call option payoff. The final column is not necessary to price the option, but it is included as a check on the drift assumption. It is a relatively straightforward way to duplicate the Black-Scholes formula without having to introduce PDEs.
Using the Black-Scholes assumptions, the spreadsheet gives a value of $11.93 compared to the actual Black-Scholes price of $11.92.
To me, the advantage of the spreadsheet is in breaking the formula into simple pieces. I like to look under the hood and see how the pieces fit together – what makes the mechanism work. In this format, it is possible to trace the assumptions through the steps of the process: stock returns, stock prices, option payoffs and weighted option payoffs. For this blog’s audience, this stuff is probably elementary, but for some people, it may help to demystify option pricing.
In this context, option pricing is a matter of adjusting the “stock return” distribution to reflect particular drift and volatility assumptions. By stepping through time or across other pricing assumptions, you can get a good idea of what is happening in the pricing mechanism. A separate figure in the book cross-references the standard stochastic stock price formulas to the spreadsheet elements.
This creates visibility into the basic components of option pricing: the option payoffs and their probabilities – in other words a random variable, where the option price is just the weighted average payoff, or the product of columns B and E.
The book expands the random variable framework to do several things. In the first part of the book, chapters 1 through 5, the visual approach is put into context compared to other pricing methods, Value-at-Risk and Conditional Value-at-Risk are explained in terms of simple lookups or slight modifications to lookups, and the formulas for the mean and standard deviation of the stock return random variable are derived that so the spreadsheet is fully functional across all Black-Scholes pricing assumptions.
In chapters 6 through 10, the random variable framework is used to present a simplified method of obtaining the lognormal distribution and then extended to a general model of options-based structured securities.
In chapters 11 through 15, the model is applied to covered calls, iron condors and synthetic annuities. There are also discussions and illustrations of analyzing option price changes and calculating greeks.
Here is a Figure from the book that illustrates the finished model for a synthetic annuity.
As another example, here is the model for a condor.
The idea behind the model is to highlight the probability curve – and how it changes over time and with different pricing assumptions – rather than obscure it inside closed-form solutions. What is surprising is how easy it is to build the model with random variables.
To make the transition between design and management, I included some material from PwSA as the last two chapters in the new book. Chapters 14 and 15 are from PwSA and talk about the practical considerations in tracking the performance of structured securities and an introduction to the design of a particular form of SynA that uses covered calls and protective puts, a form that is appropriate for more conservative investors.
Q: How can traders benefit from your book? What are the practical applications?
A: For the audience of this blog, I think there are a couple of ways. First, in managing portfolios, I think the issues around using volatility for diversification is very interesting. So far, I haven’t been able to get comfortable with any straightforward way of doing this. The first generation ETPs are very hard to use and the second generation products are still questionable in their ability to capture the right moves at low cost.
In PwSA, I devote a chapter to ideas about how a SynA might help. The chapter is called “Synthetic Annuities for the Volatility Market” and looks at an example using VXX. As I’m sure the readers of this blog know well, the challenge is to offset the high roll costs associated with holding this instrument.
The objective of a volatility-based SynA is to capture diversified returns while helping to counteract the problem of “holding” volatility. Specifically, the SynA attempts to capture the high levels of IV in short puts and short put spreads on exchange-traded instruments like the VXX. The idea is that if you can pick up theta at a rate approximately equal to the levels of negative roll yield, it can provide a useful portfolio diversifier and keep the cost of holding it down at the same time. The approach can be modified to layer in short call spreads to further counteract roll costs, especially when the level of VIX is declining, or when the shape of the curve is changing. It does require fine-tuning adjustments to improve the stability of the hedge. The same technique could be used on VXZ or other new products where options are available.
The second way, related to Visual Quantitative Finance
Visual Quantitative Finance
Subscribe to:
Posts (Atom)
Weekly market report
Wall st delivered a mixed bag of news with VIX, VNKY, and VSTOXX and their underlying markets almost unchanged. VXD - volatility index based...
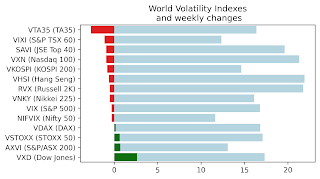
-
As I am sure all of you know Russia has began a full scale war against my home country Ukraine. Please make no mistake - Putin's goal ...
-
Another positive week for the market, and negative week for volatility. VIX and VSTOXX long term contracts continued to fall, declining by a...
-
Deutsche Bank Currency Volatility Index was developed to provide an implied volatility benchmark for major currency markets. The index is d...



