- VIX at 16 is low compared to its historical levels, but high relative to SPX vol, and vol of vol premium
- For short vol use 1:3 put spread
- For long vol use actively managed 1:2 call spread
Jeremy Wien: Utilizing the VIX Index
Jeremy Wien is truly a wellspring of practical VIX information! I posted earlier about his research here and here. Two months ago he made a presentation (with Jason Hedberg) at the CBOE Risk Management Conference, titled Utilizing the VIX Index. Here is the direct link to the presentation, below are the main points:
VIX Expiration, Week in Volatility
Last VIX expiration we were in the middle of quite frightful economic situation in the aftereffect of Japanese tsunami/earthquake and Libya, with VRO at 25.14. Now month later the market perception has sharply reversed with VIX again trading new multi-year lows. VIX settled at 14.86 on April expiration, down more than 10 points, while VSTOXX fell from 35.23 to 19.08 (closing values on Mar 16 and Apr 20). The forecasts that I made where quite off - just like I could not anticipate the rise in volatility, I really could not anticipate the fall. In my own trading I experience a very uncomfortable drawdown that I subsequently recovered from, and took opportunity to buy a lot of options during last week's decline in the VIX.
My forecasts for the next expiration are
VIX at 16.51 vs 17.90 in the futures, and
VSTOXX at 20.60 vs 21.30 in the futures



GVZ futures traded 42 contracts last week, and options volume grew as well, but for some technical reasons I cannot get the total options number. EDIT: 146 options contracts.
My forecasts for the next expiration are
VIX at 16.51 vs 17.90 in the futures, and
VSTOXX at 20.60 vs 21.30 in the futures
GVZ futures traded 42 contracts last week, and options volume grew as well, but for some technical reasons I cannot get the total options number. EDIT: 146 options contracts.
Week in Volatility
Stock Indexes were mostly down, but spot volatility was down as well. In fact it is surprising how low VIX got on Friday: closed at 15.32, intraday low was below 15! I took the opportunity to buy back a lot of options on cheap and reduce my haircut. Unfortunately at this time I don't see trades with good risk/reward ratios, my plan for the upcoming week is wait and see.
GVZ options debuted on Tuesday, and traded 70 contracts. Futures had no trades this week, open interest is unchanged at 8 contracts. The term structure of futures is practically unchanged for the week, but that means little since there is no trading activity.




GVZ options debuted on Tuesday, and traded 70 contracts. Futures had no trades this week, open interest is unchanged at 8 contracts. The term structure of futures is practically unchanged for the week, but that means little since there is no trading activity.
GVZ (GOLD VIX) Futures & Options
Well, yesterday GVZ futures traded 8 contracts, which is better than CME's GVX futures, but still far worse than VIX futures that traded over 200 contracts on their debut back in 2004. Meanwhile I came across a quality post from OptionPit that discusses trading dynamics of GLD to infer about GVZ options. For example since there is both call and put skew on GLD, GVZ will increase on down and up moves - unlike the VIX there will very little directional correlation. My only criticism is that the author writes that VIX is a vega weighted index, which is not true.
GVZ (GOLD VIX) Options To Start Trading
CFE representative privately informed me that options on GVZ - Gold volatility index will starting trading on Tuesday April 12, 2011. Group One, current DPM for VIX options will be DPM for GVZ options as well. There is still no LMM for the futures.
Edit: Official press release from CBOE.
Edit: Official press release from CBOE.
Week in Volatility
Rather uneventful week for volatility - it seems that the markets are back to what they were doing before tsunami. I traded defensively as planned, reducing the short contracts count in June, and spreading it against near-term.
The Probability And Expected Return, Part 1
Many option traders look at delta as indicator of probability of potential payoff, however are not aware of that payoff's magnitude. They make qualitative judgments and use vague rules for decision making. For example a seller of OTM options will tell you that the odds of going in the money are only 10%, so he’ll make money approximately (adjusting by premium and trading costs) 90% of the time. Such simplistic thinking however does not take into account what exactly will happen if option goes in the money. The concept that I'm explaining here is not some high-level math, but rather a simple and fast rule of thumb that can be easily used in practical trading.
With the usual Black-Scholes assumptions:
Option price = E[Discount * Max(S-K,0)], where S is the stock price as expiration, E is the expectation operator, P is the probability, Discount is exp(-rT) . Max(S-K,0) is a payoff of a call option at expiration; similar analysis will hold for puts. In simple words, the options price today is how much you would expect it to be worth at expiration, discounted by interest rate. For simplicity I'll ignore the discount factor.
Option price = E[Max(S-K,0)] =
E[Max(S-K,0)|S>K] * P[S>K]
+ E[Max(S - K,0)|S<=K] * P[S<=K].
It means that the options price is equal to its expected payoff in the money multiplied by the probability of being in the money, and its expected payoff out of the money multiplied by the probability of being out of the money. Because option is not worth anything when it is out of the money, the second term is zero.
Option price = E[Max(S-K,0)] = E[Max(S-K,0) |S>K] * P[S>K]
The last term is the delta of the option. Now we can invert the equation, obtaining
E[Max(S-K,0) |S>K] = E[Max(S-K,0)] / P[S>K] = E [Max(S-K,0)] /Δ
The option payoff conditioned on it finishing in the money is option price divided by delta.
Example:
The current price of an asset is $100, strike is $130, interest rate is 10%, and time to maturity is ¼ year. The option trades at $0.80, or at 35% annual volatility. Delta of the option is 10%. While the option will let the seller collect premium 90% of the time, the seller faces a potential risk of losing the premium and more if the option goes in the money. This value is $0.80/0.1 = $8.00
Selling this option can be thought of as making a binary bet that will pay $0.80 90% of the time, and lose $7.20 10% of the time. Simple calculation 0.8*0.9 – 7.2*0.1 = 0 confirms that it is a fair bet.
With the usual Black-Scholes assumptions:
Option price = E[Discount * Max(S-K,0)], where S is the stock price as expiration, E is the expectation operator, P is the probability, Discount is exp(-rT) . Max(S-K,0) is a payoff of a call option at expiration; similar analysis will hold for puts. In simple words, the options price today is how much you would expect it to be worth at expiration, discounted by interest rate. For simplicity I'll ignore the discount factor.
Option price = E[Max(S-K,0)] =
E[Max(S-K,0)|S>K] * P[S>K]
+ E[Max(S - K,0)|S<=K] * P[S<=K].
It means that the options price is equal to its expected payoff in the money multiplied by the probability of being in the money, and its expected payoff out of the money multiplied by the probability of being out of the money. Because option is not worth anything when it is out of the money, the second term is zero.
Option price = E[Max(S-K,0)] = E[Max(S-K,0) |S>K] * P[S>K]
The last term is the delta of the option. Now we can invert the equation, obtaining
E[Max(S-K,0) |S>K] = E[Max(S-K,0)] / P[S>K] = E [Max(S-K,0)] /Δ
The option payoff conditioned on it finishing in the money is option price divided by delta.
Example:
The current price of an asset is $100, strike is $130, interest rate is 10%, and time to maturity is ¼ year. The option trades at $0.80, or at 35% annual volatility. Delta of the option is 10%. While the option will let the seller collect premium 90% of the time, the seller faces a potential risk of losing the premium and more if the option goes in the money. This value is $0.80/0.1 = $8.00
| Probability | Result | Expected Payoff |
| 90% | Collect premium | $0.80 |
| 10% | Lose premium, or more | $0.80-$8.00=-$7.20 |
Selling this option can be thought of as making a binary bet that will pay $0.80 90% of the time, and lose $7.20 10% of the time. Simple calculation 0.8*0.9 – 7.2*0.1 = 0 confirms that it is a fair bet.
Subscribe to:
Posts (Atom)
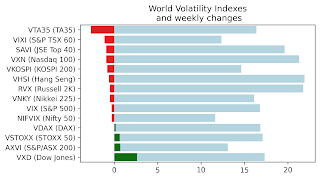
Weekly market report
Wall st delivered a mixed bag of news with VIX, VNKY, and VSTOXX and their underlying markets almost unchanged. VXD - volatility index based...
-
As I am sure all of you know Russia has began a full scale war against my home country Ukraine. Please make no mistake - Putin's goal ...
-
Another positive week for the market, and negative week for volatility. VIX and VSTOXX long term contracts continued to fall, declining by a...
-
Deutsche Bank Currency Volatility Index was developed to provide an implied volatility benchmark for major currency markets. The index is d...