Risk: Asia-specific Vix indexes fail to ignite market interest.
The title pretty much says it all, that outside US and VSTOXX on Eurex volatility futures have not taken off. Will this change now since CBOE introduced (almost) 24-hour trading in VIX futures? Will arbitrageurs add liquidity to Asian products, or will Asian hedgers flock to VIX to manage risk? Only time will tell.
More Intuition On Volatility And Square Root Of Time
Vance at Six Figure Investing recently wrote an excellent post titled Volatility and the Square Root of Time. I would like to try to add a little more intuition about this particular theoretical property of gaussian random walk process, or Wiener process.
If we gloss over technical details Wiener process can be described as a sum of random draws from normal distribution - that is starting at 0 we keep adding a new random number at each time step. However we are going simplify this even further, and will use even more basic process - starting at 0, at each time step we flip a coin, and with heads we add 1, with tails we subtract one. And although this may sound like a grade-school version of Wiener process this is actually a valid "substitute" for our purposes.
 Here I plotted some sample paths. And yes, this binomial walk looks quite like gaussian random walk.
Here I plotted some sample paths. And yes, this binomial walk looks quite like gaussian random walk.
Now we will look at the process in greater detail, and specifically we will look at the volatility of the process at each time step.
So, we take the first step, and calculate expected variance as sum of squared values multiplied by probabilities. In this case we get (1)2 * ½ + (-1)2 * ½ = 1. So, t=1, variance=1, volatility=√1=1 . Ok, one
After 2 steps we have 3 values, and 4 distinct paths: +1 + 1 = 2, +1 -1 = 0, -1 + 1 = 0, and -1 -1 = -2. We use the same method to calculate variance: (2)2 * ¼ + (0)2 * ½ + (-2)2 * ¼ = 1 + 1 = 2. So, t=2, variance=2, volatility=√2 . Ok, let's do one more step:
After 3 steps we have 4 values, and 8 distinct paths which I am not going to enumerate; count for yourself. We use the same method to calculate variance: (3)2 * ⅛ + (1)2 * ⅜ + (-1)2 * ⅜ + (-3)2 * ⅛ = 9/8 + 3/8 + 3/8 + 9/8 = 24/8 = 3. So, t=3, variance=3, volatility=√3
As you can see variance scales with time, while volatility scales with its square root. I should point out that volatility is not the only quantity to scale with the √t, the property also holds true for expected high, expected low, expected range, expected drawdown and drawup - they all scale the same way, as I wrote in another post.
 Finally, Vance writes that the relationship approximately holds for options (assuming no rates and no dividends). I would clarify: it holds approximately assuming small rates, small dividends, and small volatility. Also it holds much better for ATM options, but not so much when you move away from the money.
Finally, Vance writes that the relationship approximately holds for options (assuming no rates and no dividends). I would clarify: it holds approximately assuming small rates, small dividends, and small volatility. Also it holds much better for ATM options, but not so much when you move away from the money.

If we gloss over technical details Wiener process can be described as a sum of random draws from normal distribution - that is starting at 0 we keep adding a new random number at each time step. However we are going simplify this even further, and will use even more basic process - starting at 0, at each time step we flip a coin, and with heads we add 1, with tails we subtract one. And although this may sound like a grade-school version of Wiener process this is actually a valid "substitute" for our purposes.
 Here I plotted some sample paths. And yes, this binomial walk looks quite like gaussian random walk.
Here I plotted some sample paths. And yes, this binomial walk looks quite like gaussian random walk.Now we will look at the process in greater detail, and specifically we will look at the volatility of the process at each time step.
| t=0 | t=1 | probability |
|---|---|---|
| +1 | ½ | |
| 0 | ||
| -1 | ½ |
| t=0 | t=1 | t=2 | probability |
|---|---|---|---|
| +2 | ¼ | ||
| +1 | |||
| 0 | 0 | ½ | |
| -1 | |||
| -2 | ¼ |
After 2 steps we have 3 values, and 4 distinct paths: +1 + 1 = 2, +1 -1 = 0, -1 + 1 = 0, and -1 -1 = -2. We use the same method to calculate variance: (2)2 * ¼ + (0)2 * ½ + (-2)2 * ¼ = 1 + 1 = 2. So, t=2, variance=2, volatility=√2 . Ok, let's do one more step:
| t=0 | t=1 | t=2 | t=3 | probability |
|---|---|---|---|---|
| +3 | ⅛ | |||
| +2 | ||||
| +1 | +1 | ⅜ | ||
| 0 | 0 | |||
| -1 | -1 | ⅜ | ||
| -2 | ||||
| -3 | ⅛ |
After 3 steps we have 4 values, and 8 distinct paths which I am not going to enumerate; count for yourself. We use the same method to calculate variance: (3)2 * ⅛ + (1)2 * ⅜ + (-1)2 * ⅜ + (-3)2 * ⅛ = 9/8 + 3/8 + 3/8 + 9/8 = 24/8 = 3. So, t=3, variance=3, volatility=√3
As you can see variance scales with time, while volatility scales with its square root. I should point out that volatility is not the only quantity to scale with the √t, the property also holds true for expected high, expected low, expected range, expected drawdown and drawup - they all scale the same way, as I wrote in another post.
Subscribe to:
Posts (Atom)
Weekly market report
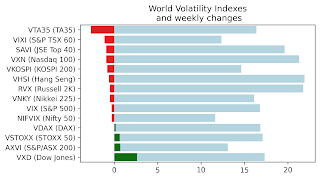
Wall st delivered a mixed bag of news with VIX, VNKY, and VSTOXX and their underlying markets almost unchanged. VXD - volatility index based...
-
As I am sure all of you know Russia has began a full scale war against my home country Ukraine. Please make no mistake - Putin's goal ...
-
Another positive week for the market, and negative week for volatility. VIX and VSTOXX long term contracts continued to fall, declining by a...
-
Deutsche Bank Currency Volatility Index was developed to provide an implied volatility benchmark for major currency markets. The index is d...