OnlyVIX: Thank you very much for agreeing to this interview. Let’s start at the beginning - how did you come to become a market-maker in such an exotic product? Your background is in bond/bond derivatives trading, and you worked at some big funds. Did you see a big opportunity for Shiller Index futures in general, or a niche for yourself?
John Dolan: I actually backed into this role as it fit a number of my interests. During 2006, in my capacity of Chief Investment Officer of a $20 billion asset management company that focused on deep RMBS credit (Hyperion-Brookfield Asset Management) I certainly had paid attention to the roll-out of housing futures. At the time, I thought this was a useful tool, as while MBS analysts had models that predicted prepayment projections with incredible precision most of what you heard about home prices was that there had never been a national decline in home prices, and much of "analysis" ended at that. There had been good (appropriate) awareness that increases in home price drove mortgage refinancing - which was generally good for RMBS credit, but most of what you read at the time was that home prices might rise between 5 and 10%. In theory, the Case Shiller futures would become a market for public expectations.
Unfortunately (for the CME contracts), portfolio managers’ attention and trading shifted to the OTC ABX credit-default swaps (a more lucrative business for Wall Street, that better hedged their positions) and interest in the Case Shiller futures became incredibly one-sided (i.e. mostly sellers).
I left the asset management business in 2007 and found my way to litigation consulting, and eventually expert witness work (which I continue to do today, along with teaching). Many of the questions in 2007-2009 were of a Watergate-like mindset, "what did they know and when did they know it?" I became interested in addressing that question as it related to the decline in home prices, and thought that the futures (which were forward looking) might have given an earlier signal than the commonly referenced housing indices (as most were moving averages issued with a lag).
So as a former trader, and huge fan of futures as a hedge (I've traded gas, FX, S&P, T-bonds, coffee and cattle in my PA) I looked into the contracts and noticed that they were quoted with very large bid/ask spreads – almost 20 points in some cases, and in other there were no quotes at all. Also forward curves had no consistent message - closes indicated that forward prices would be higher or lower, or in some cases both, with different slopes for different regions. Having seen just what had happened in the 2006-07 housing collapse I thought that the market (and distressed RMBS and Whole Loan buyers) might be well served by a more robust market for housing futures, so I started bidding and offering.
After a while I grew frustrated that there were so few responses (counters) so I called the CME to inquire. They told me that all of the market makers had either re-prioritized their efforts, or had left their firms, and that in fact there was no real market maker. I don't recall who asked first, but I figured that if I was taking the risk of making markets, that I might as well have the upside of being known for that. That role continues to open doors to meetings that might otherwise be a challenge to arrange.
And that's how I came to be the market maker in 2010.
OV: So now you have been doing it for five years; how is it working out?
JD: At one point I became quite obsessed with making sure that there were prices on all 121 contracts (11 regions* 11 expirations). I think that may have diffused some potential trading interest, so later (and through today) I decided to just be more responsive to, and offer better quotes on, inquiries, offer a tighter set of bids and offers for the first 5 expirations (while continuing to maintain a full set on the 10-city index). Bid/ask spreads are at historical narrow levels. I try to keep at least one CUS contract (10-city index) under one point (bid/ask).
In the last five years I encouraged the CME to switch from having the contracts open 21 hours/day to today's ~8 hours, and also worked with the CME to reintroduce electronic options (but only on 4 regions to focus interest.). However, that effort only resulted in one sizeable trade (35 lots) in 2014. (BTW- I am taking another run at that with focus on the LAX Nov' 17 contract.)
OV: I can imagine that risk management can be quite difficult - there is no forward arbitrage (like VIX index, and other non-store-able commodities). Also, for you as a market maker there are additional issues (correct me if I'm wrong) – trading is sparse, and city-indexes are not correlated with anything?
JD: Yes, I have often been > 50% of quotes and open interest for last few years, there is no cash (OTC) market, and as such, there is no one to hedge with. Beyond that, I've analyzed that home price futures are not highly correlated with anything. So, maybe a good portfolio tool, but a lousy product to hedge.
For now, I just try not to get offside by more than 30 contracts ($1.5mm position) and try to bias the markets I quote to be more likely to get back to even.
Net, I use the market making role to be the sounding board for parties looking for other sides to trade with, and, in the past, have come close to brokering 50+ lots. Keeping quotes posted keeps me current on issues related to home prices, which helps in other parts of my consulting business.
Success to me would be having some Wall Street firm realize the potential, make very tight 10x10 markets, and find a use for the futures in other products (e.g. an ETF, capital relief, etc.)
OV: So if this is such a big market AND if people have very recent memories of taking big losses, why is there not more trading in these futures?
JB: While there is some element of chicken-and-egg (i.e. limited trading because people don't see others trading) I sense that there may be a few other good reasons:
In my experience in talking to potential traders, while hedgers are happy to hedge using an index, most longs seem to be less enthusiastic about buying an index. Real estate longs feel that it’s all about “location, location, location” and as such, active management (e.g. asset picking) prevails. While there have been periods where asset selection provided great opportunities (e.g. S&L crises, post the 2007 crash), I tend to think that the equivalent of passive management, i.e. buying the performance of an index via a futures contract should appeal to some potential longs at some points in time.
Case Shiller futures represent the price of the index at a point in time. Unfortunately, some longs would like to buy the spot index, and carry it (to ride the price rise), but can’t replicate that via futures. Unlike forward S&P500 contracts, which trade versus spot based on carry (and anticipated dividends) Case Shiller futures are not spot levels carried forward. One-year forward futures prices were ~8% higher than spot in 2012 reflecting a belief that the turn had come and that the percent of assets sold at distressed levels would decline.
Home price futures have exhibited almost no correlation to the stock market over the last two years. For example, the S&P is up ~300 points and the CUSX16 (10-city contract for Nov ’16) is flat. Traders express frustration that the futures can’t be hedged. Great, I say, because as a portfolio manager I want assets that have low R^2 to the stock market.
A final angle is that there’s an element that the futures are “too good” a hedging asset. Someone looking to hedge against a price decline could sell Nov ’17 contracts and never have to roll the position. While that might work well for a hedger, the futures broker won’t see much trading. Brokers seem to prefer day traders and tight, deep markets.
Finally, I think that options, rather than futures might be a better retail product. I’m working on that.
OV: Thank you very much, John!
John Dolan's website is HomePriceFutures.com where he writes about home price derivatives.
Some Vol Funds News
FINalternatives reports that recent large trades in crude may be linked to liquidation of Blueshift Energy Fund. New-York based fund had a strong start, returning 15% in its first 7 months of trading in 2013, and 9% in 2014. According to most recent fund data, the fund was managing $170M but had a difficult year, losing 8% in March, and being down more than 9% this year.
FINalternatives article. Fiscal times article
Blackheath Volatility Arbitrage Strategy is also apparently closing out - the fund information was removed from website leaving other two funds. Funds performance has been rocky - it lost 4% in 2013, 5% in 2014, and is down 23% for 2015.
True Partner Capital is expanding, and planing to open US office in Chicago. Hong-Kong based volatility fund profited from the turbulent markets 2 months, up 15% on the year according to recent bloomberg article. The fund was recently a winner of AsiaHedge 2015 award in the market neutral and arbitrage fund category.
FINalternatives article. Fiscal times article
Blackheath Volatility Arbitrage Strategy is also apparently closing out - the fund information was removed from website leaving other two funds. Funds performance has been rocky - it lost 4% in 2013, 5% in 2014, and is down 23% for 2015.
True Partner Capital is expanding, and planing to open US office in Chicago. Hong-Kong based volatility fund profited from the turbulent markets 2 months, up 15% on the year according to recent bloomberg article. The fund was recently a winner of AsiaHedge 2015 award in the market neutral and arbitrage fund category.
MLKJ Day
Few months ago I posed a quick note on date count as it relates to MLKJ day. Recently I received an email from Luigi Ballabio that correction has been accepted and will become part of Quantlib 1.7. Thanks to John Orford for the suggestion!
Volatility and the Allegory of the Prisoner's Dilemma
While I try to focus on original research on this blog, I cannot pass up opportunity to share this new research piece from Chris Cole of Artemis Capital - Volatility and the Allegory of the Prisoner's Dilemma. It is, as always, excellent.
Global Sigma Group, St Crispin's Day Speech
Global Sigma Group, a volatility fund with almost 6 years track record in S&P options is preparing a new offering called BondVol, with focus on Treasuries vol. New information, although quite sparse, is available on their website, as well as this SEC filing. One interesting point is -86% correlation between Sigma Plus and BondVol funds, but I believe this to be a statistical fluke - knowing the factor drivers of such strategies I believe that long-term correlation will be positive, and significant, probably at +50%.
The (unconfirmed) rumor is that the flagship Global Sigma Plus Program is suffering their largest drawdown to date, although my understanding is that it is significant, but within reason. I know a many people in volatility space, and August has been difficult for many, and everyone knows that they can't all be winners. So, fellow traders - hedge your deltas, and good luck in September. Remember, you may have lost money, but not ability to make money.
The (unconfirmed) rumor is that the flagship Global Sigma Plus Program is suffering their largest drawdown to date, although my understanding is that it is significant, but within reason. I know a many people in volatility space, and August has been difficult for many, and everyone knows that they can't all be winners. So, fellow traders - hedge your deltas, and good luck in September. Remember, you may have lost money, but not ability to make money.
Capstone Is Having A Great Month
According to today's article in Business Insider Australia, Capstone (largest dedicated volatility trading hedge fund) is having a great month.
I don't have access to Capstone returns, so these numbers are interesting, to analyze and compare to how other vol funds did in August.
"One of the smaller funds in the firm’s tail risk strategy has delivered a 55% return so far this month, according to a person familiar with the fund’s returns. Across that strategy, Capstone manages $US600 million. The 55% is for one of those funds.
The firm’s bigger $US3 billion flagship volatility arbitrage fund return 1.2% so far in August, according to the person."The rest of the article is hand wavy explanation of volatility and trading.
I don't have access to Capstone returns, so these numbers are interesting, to analyze and compare to how other vol funds did in August.
More on CBOE's Buy-Write Indexes
As I mentioned in the previous post, it is not easy to separate real alpha, from mean-median difference in short gamma strategies. Since buy-write strategies are short gamma, it is not surprising that they show alpha in regression. This is the table that I calculated in the previous post.
As we can plainly see, adding PUT as factor significantly reduces alphas, and their t-stats. Not only BXM - which is by construction (pretty much) a linear combination of PUT and SPX has no alpha, but also other benchmark "innovations" - BXMC (conditional) or BXY (2% otm) do not provide any meaningful alpha. The only two benchmarks standing out now is BXMW - which has relatively short history, and BXMD (30-delta buy-write).
| Symbol | Start Date | Annualized Alpha | Beta SPX | Alpha t-stat |
|---|---|---|---|---|
| BXM | 30-Jun-86 | 3.8% | 0.66 | 3.88 |
| BXMC | 31-Jan-90 | 4.5% | 0.69 | 4.75 |
| BXMD | 30-Jun-86 | 4.1% | 0.83 | 4.60 |
| BXMW | 29-Jun-12 | 2.3% | 0.61 | 1.57 |
| BXY | 1-Jun-88 | 4.3% | 0.76 | 4.40 |
How will these results change if we add another (systematic short volatility) factor into regression. For that factor I will use CBOE's own PUT index, which sells monthly atm puts.
| Symbol | Start Date | Annualized Alpha | Beta SPX | Alpha t-stat |
|---|---|---|---|---|
| BXM | 30-Jun-86 | 0.3% | 0.25 | 0.66 |
| BXMC | 31-Jan-90 | 0.7% | 0.29 | 1.31 |
| BXMD | 30-Jun-86 | 1.8% | 0.57 | 2.57 |
| BXMW | 29-Jun-12 | 2.0% | 0.29 | 2.10 |
| BXY | 1-Jun-88 | 0.8% | 0.41 | 1.16 |
As we can plainly see, adding PUT as factor significantly reduces alphas, and their t-stats. Not only BXM - which is by construction (pretty much) a linear combination of PUT and SPX has no alpha, but also other benchmark "innovations" - BXMC (conditional) or BXY (2% otm) do not provide any meaningful alpha. The only two benchmarks standing out now is BXMW - which has relatively short history, and BXMD (30-delta buy-write).
Quick Note on CBOE's Buy-Write Indexes
Last month CBOE expanded their portfolio of benchmark indexes, adding 10 more new ones. Link to the press release. I would not be surprised that some people will look at these benchmarks as complete trading strategies, however one should be careful as such benchmark indexes are often just an exercise in overfitting until desired result (pretty chart) can be produced.
Such datamining error is especially easy with options. Short strategies tend to produce "good" results that seem like a legitimate alpha, when in reality it is just the median returns are high, and average returns looks much worse, i.e. the strategy negatively skewed. Even when one is using a long dataset, for example including the crisis of 2008, it is too easy to add a moving average filter, or change parameters in such a way as to create good results.
Separating legitimate alpha, especially short volatility alpha from what is generally referred to "volatility risk premium" is difficult. I believe if one is facing such task, the process should be both quantitative and qualitative, checking that the strategy makes sense on the logical level. Here I will not try to perform any thorough analysis but will just add a few notes and ides on the new benchmarks.
As I mentioned above there were total of 10 new strategies, 9 based on SPX, and one based on VIX. Complete list of CBOE benchmarks is available here. I will start with buy-write indexes, but will write about other benchmarks in later posts.
And indeed the weekly buy write outperforms BXM - alpha (to BXM, not SPX) is 3% annualized with beta of about 0.9. Most of the outperformance comes from two periods: in the end of 2012 and most recently in October of 2014. The drawdowns seems to be about the same, however BXMW has stronger rebounds than BXMW. Below are all three indexes for comparison.
Such datamining error is especially easy with options. Short strategies tend to produce "good" results that seem like a legitimate alpha, when in reality it is just the median returns are high, and average returns looks much worse, i.e. the strategy negatively skewed. Even when one is using a long dataset, for example including the crisis of 2008, it is too easy to add a moving average filter, or change parameters in such a way as to create good results.
Separating legitimate alpha, especially short volatility alpha from what is generally referred to "volatility risk premium" is difficult. I believe if one is facing such task, the process should be both quantitative and qualitative, checking that the strategy makes sense on the logical level. Here I will not try to perform any thorough analysis but will just add a few notes and ides on the new benchmarks.
As I mentioned above there were total of 10 new strategies, 9 based on SPX, and one based on VIX. Complete list of CBOE benchmarks is available here. I will start with buy-write indexes, but will write about other benchmarks in later posts.
"The CBOE S&P 500 Multi-Week BuyWrite Index is designed to track the performance of a hypothetical weekly covered call strategy with staggered short positions in call options expiring in consecutive four week options. The BXMW Index is constructed as a combined portfolio of four mini BuyWrite indexes. Expirations are staggered so that the BXMW Index sells four-week options on a rolling weekly basis. "
This is a very recent index, and CBOE obviously tried to generalize the "original" Buy Write by using weeklys. In-samples statistics are robust - the benchmark delivers about 2% annualized alpha, with 0.6 beta to SPX. Of course it is more interesting is writing weeklys is better than writing regular monthly options, so let's compare BXMW to BXM.And indeed the weekly buy write outperforms BXM - alpha (to BXM, not SPX) is 3% annualized with beta of about 0.9. Most of the outperformance comes from two periods: in the end of 2012 and most recently in October of 2014. The drawdowns seems to be about the same, however BXMW has stronger rebounds than BXMW. Below are all three indexes for comparison.
"The CBOE S&P 500 30-Delta BuyWrite Index is designed to track the performance of a hypothetical covered call strategy that holds a long position indexed to the S&P 500 Index and sells a monthly out-of-the-money (OTM) S&P 500 Index (SPX) call option. The call option written is the strike nearest to the 30 Delta at 10:00 a.m. CT on the roll date. The BXMD Index rolls on a monthly basis, typically every third Friday of the month. "BXMD writes a call that is father OTM than the original BXM. Not surprisingly alpha is higher - or let's say full premium is collected more often, alpha in the regression is higher, not necessarily true alpha. Beta is higher, as expected. Another very similar index is BXY, which uses 2% instead of 30-delta rule. BXY does just a tiny bit worse than BXMD, but the difference is not significant, so I will not include the chart.
"The CBOE S&P 500 Conditional BuyWrite Index is designed to track the performance of a hypothetical covered call strategy that holds a long position indexed to the S&P 500 Index and sells a monthly at-the-money (ATM) S&P 500 Index (SPX) call option. The written number of ATM call options will be either ½ unit or 1 unit and will be determined by the level of the CBOE Volatility Index (VIX Index) when the call option is written on the roll date. The BXMC Index rolls on a monthly basis, typically every third Friday of the month. "
BXMC writes more or less options depending in the VIX level. It is not a surprise that adding this rule improves performance with alpha of 4% and beta of 0.7.
| Symbol | Start Date | Annualized Alpha | Beta | Alpha t-stat |
|---|---|---|---|---|
| BXM | 30-Jun-86 | 3.8% | 0.66 | 3.88 |
| BXMC | 31-Jan-90 | 4.5% | 0.69 | 4.75 |
| BXMD | 30-Jun-86 | 4.1% | 0.83 | 4.60 |
| BXMW | 29-Jun-12 | 2.3% | 0.61 | 1.57 |
| BXY | 1-Jun-88 | 4.3% | 0.76 | 4.40 |
There is really nothing surprising about these summary stats - beta < 1, alpha > 0 (otherwise there would be no benchmark), and ones with more rules make more alpha. However selling otm index calls (against the skew) is obviously risky in the run-away bull market like we had in the past few years. So let's see how the benchmarks fared over the most recent period (same as BXMW which has the shortest history)
| Symbol | Start Date | Annualized Alpha | Beta | Alpha t-stat |
|---|---|---|---|---|
| BXM | 29-Jun-12 | -0.9% | 0.65 | -0.51 |
| BXMC | 29-Jun-12 | -0.4% | 0.80 | -0.32 |
| BXMD | 29-Jun-12 | -0.9% | 0.81 | -0.59 |
| BXMW | 29-Jun-12 | 2.3% | 0.61 | 1.57 |
| BXY | 29-Jun-12 | -1.8% | 0.85 | -1.17 |
I guess this is really the main reason for introduction of the BXMW - it is the only benchmark to beat SPX! To be honest, I am not sure why this is so - why is monthly sale worse than 4 weekly sales? What is it in the skew that would explain this outperformance? I don't know - and I would not really put much trust that this recent performance by BXMW is robust. I do not believe that there is sufficient evidence that buy-write indexes are delivering true alpha - or enough alpha to justify beta risk.
For further reading (and more optimistic view) I recommend this recent article.
YLDVOL - Better Fixed Income Volatility Index
By all accounts CBOE's VXTYN Index has been a bust in terms of market participation. Currently the front month contract has zero volume, and zero open interest. This is where Triple 3 Partners, Australia-based hedge fund manager specializing in volatility trading, is hoping to step in.
They have developed an alternative index YLDVOL (Bloomberg ticker YLDVUST) that i s supposed to better represent hedging and speculation needs of fixed income traders. YLDVOL has been developed under guidance of Dr Peter Carr from academic side, and in consultation with many fixed income traders.
What traders complained about, is that CBOE just took their existing (admittedly very successful) VIX Index formula, and copied and pasted it to treasury market, ignoring specific differences between equities and FI. The differences are far from superficial - while equities volatility is typically quoted in %s, FI vol is quotes in basis points. This is really not just about the denominator, percent vol presumes geometric process (like geometric Brownian motion) while points vol presumes arithmetic process (like "regular" arithmetic Brownian motion). Therefore it would make sense that instead of VAR-Swap formula that is used for VIX index, YLDVOL would use Bachelier's implied vol. Just like the VIX, YLDVOL is interpolated to a constant 30-day maturity.
Details on the index, and index calculations are available on t3index.com, and live values on Bloomberg using YLDVUST Index. A look-alike index based on BUND with Bloomberg ticker YLDVBUND Index.
They have developed an alternative index YLDVOL (Bloomberg ticker YLDVUST) that i s supposed to better represent hedging and speculation needs of fixed income traders. YLDVOL has been developed under guidance of Dr Peter Carr from academic side, and in consultation with many fixed income traders.
What traders complained about, is that CBOE just took their existing (admittedly very successful) VIX Index formula, and copied and pasted it to treasury market, ignoring specific differences between equities and FI. The differences are far from superficial - while equities volatility is typically quoted in %s, FI vol is quotes in basis points. This is really not just about the denominator, percent vol presumes geometric process (like geometric Brownian motion) while points vol presumes arithmetic process (like "regular" arithmetic Brownian motion). Therefore it would make sense that instead of VAR-Swap formula that is used for VIX index, YLDVOL would use Bachelier's implied vol. Just like the VIX, YLDVOL is interpolated to a constant 30-day maturity.
Details on the index, and index calculations are available on t3index.com, and live values on Bloomberg using YLDVUST Index. A look-alike index based on BUND with Bloomberg ticker YLDVBUND Index.
Frontiers in Time Series and Financial Econometrics
While I try to focus on original content on this blog, this paper is an excellent overview of latest developments in financial time series.
Abstract:
Abstract:
Two of the fastest growing frontiers in econometrics and quantitative finance are time series and financial econometrics. Significant theoretical contributions to financial econometrics have been made by experts in statistics, econometrics, mathematics, and time series analysis. The purpose of this special issue of the journal on “Frontiers in Time Series and Financial Econometrics” is to highlight several areas of research by leading academics in which novel methods have contributed significantly to time series and financial econometrics, including forecasting co-volatilities via factor models with asymmetry and long memory in realized covariance, prediction of Lévy-driven CARMA processes, functional index coefficient models with variable selection, LASSO estimation of threshold autoregressive models, high dimensional stochastic regression with latent factors, endogeneity and nonlinearity, sign-based portmanteau test for ARCH-type models with heavy-tailed innovations, toward optimal model averaging in regression models with time series errors, high dimensional dynamic stochastic copula models, a misspecification test for multiplicative error models of non-negative time series processes, sample quantile analysis for long-memory stochastic volatility models, testing for independence between functional time series, statistical inference for panel dynamic simultaneous equations models, specification tests of calibrated option pricing models, asymptotic inference in multiple-threshold double autoregressive models, a new hyperbolic GARCH model, intraday value-at-risk: an asymmetric autoregressive conditional duration approach, refinements in maximum likelihood inference on spatial autocorrelation in panel data, statistical inference of conditional quantiles in nonlinear time series models, quasi-likelihood estimation of a threshold diffusion process, threshold models in time series analysis - some reflections, and generalized ARMA models with martingale difference errors.
Quick Note on MLKJ Day
While president Reagan signed the holiday into law in 1983, NYSE did not make it a full-day exchange holiday until 1998. Source.
If you are asanal meticulous as me about having proper implied volatility numbers, time to expiration (that is normal expected time to expiration) these things matter. The last time I checked popular financial library quantlib their US calendar implementation, it had MLKJ day as holiday every year, even before 1998.
If you are as
Volatility Conversion
Re:Simple Trick to Convert Volatility
Reader asks, "I have weekly volatilities over 370 weeks, I like to convert this into an annualized volatility. How does this work?"
Since volatility is weekly, in the linear case the multiplier would be 52 (weeks per year) , so for volatility you should multiply your weekly volatility by √ 52.
In fact, the length of the measurement - 370 weeks - does not matter at all. If you would have 3 weeks or 7 weeks of weekly volatilities, multiplier would be the same. It is the frequency of observation that matters. To illustrate this consider another example: you have daily volatility over 370 weeks. To annulalize, multiply your daily volatility by √ 252 where 252 is the usual number of trading days per year in the US.
Reader asks, "I have weekly volatilities over 370 weeks, I like to convert this into an annualized volatility. How does this work?"
Since volatility is weekly, in the linear case the multiplier would be 52 (weeks per year) , so for volatility you should multiply your weekly volatility by √ 52.
In fact, the length of the measurement - 370 weeks - does not matter at all. If you would have 3 weeks or 7 weeks of weekly volatilities, multiplier would be the same. It is the frequency of observation that matters. To illustrate this consider another example: you have daily volatility over 370 weeks. To annulalize, multiply your daily volatility by √ 252 where 252 is the usual number of trading days per year in the US.
Another Vol Arb Mutual Fund
Recent press release from Franklin K2 Alternative Strategies Fund (Canada) shows that one of the sub-managers trades volatility arbitrage strategies. There are four "candidates" and googling suggests that Basso Capital Management is the manager running volatility strategy. Performance of the fund has been lackluster, and management fees are quite high.
Dr John Nash Dies in Crash
Dr John Nash, who made pivotal contributions to game theory and differential equations was killed on Saturday in an automobile accident with his wife Alicia. He received a Nobel Prize in economics for his work in the theory of non-cooperative games. Nash equilibrium has been applied to modelling company merges and takeovers, portfolio optimization, and algorithmic trading.
Bloomberg article.
Bloomberg article.
VIX Weeklys
VXST options looked like a great product on paper - cheap, short term options, massive mean-reversion, huge gamma - however trading just did not take off. Now CBOE is trying different angle - similar to regular weeklys, the exchange is launching weekly VIX futures, and weekly VIX options. To clarify - these are not weekly options on VXST, they are not weekly futures options (like CBOE proposed some while ago). These are options on the VIX index, just with more frequent expirations.
Officail product page. Hat tip to Nakul Nayyar.
Officail product page. Hat tip to Nakul Nayyar.
Alternatives To Matlab
Reader Eli asked in the comments "I used to program in Matlab a lot in the past. Now I feel that Python is a better way to go. Any thoughts?
Yes, quite a few - however I also hope to hear some ideas from other readers. Matlab is an excellent tool for analytics, and I have been using it for over a decade now. However if I were starting out in quantitative finance today I would probably go with Python. The main reason: Python is more popular - and bigger community means more ideas being exchanged, and potentially more job prospects. I get calls from recruiters telling me that quite a few banks have switched to Python as their main analytics tool.
However I am not ditching Matlab just yet. In my experience, Python is still much slower, more bloated, not as well documented as Matlab. Matlab is the Ferrari, where Python is basic Ford. The firm were I work pays for the license, for which I am immensely grateful!
The real question is, what's next? Matlab is not cheap, and it is important to stay on top of the latest tools. I suspect that Python will continue growing in popularity over Matlab.
But I think there are more interesting tools in development:
1 - Julia
2 - F# programming language. In particular I have been experimenting with FCore linear algebra library as stand-in for Matlab. Not all Matlab features are implemented, but basic support for logical indexing exists, and I was able to add simple custom functions to fill in whatever functionality I needed. Regression tools seem better that other .net linear algebra packages. I hope to write more about this in the future posts.
What tools are you using? Please share in the comments!
Yes, quite a few - however I also hope to hear some ideas from other readers. Matlab is an excellent tool for analytics, and I have been using it for over a decade now. However if I were starting out in quantitative finance today I would probably go with Python. The main reason: Python is more popular - and bigger community means more ideas being exchanged, and potentially more job prospects. I get calls from recruiters telling me that quite a few banks have switched to Python as their main analytics tool.
However I am not ditching Matlab just yet. In my experience, Python is still much slower, more bloated, not as well documented as Matlab. Matlab is the Ferrari, where Python is basic Ford. The firm were I work pays for the license, for which I am immensely grateful!
The real question is, what's next? Matlab is not cheap, and it is important to stay on top of the latest tools. I suspect that Python will continue growing in popularity over Matlab.
But I think there are more interesting tools in development:
1 - Julia
2 - F# programming language. In particular I have been experimenting with FCore linear algebra library as stand-in for Matlab. Not all Matlab features are implemented, but basic support for logical indexing exists, and I was able to add simple custom functions to fill in whatever functionality I needed. Regression tools seem better that other .net linear algebra packages. I hope to write more about this in the future posts.
What tools are you using? Please share in the comments!
MATLAB Computational Finance Conference 2015
MATLAB Computational Finance Conference was a great event that I attended last year. There is a lot to learn for average Matlab user, and anyone working in finance. The agenda looks especially exciting this year. Ping me if you want to meet during the event.
Volatility Arbitrage Mutual Fund?
Indeed; just came across this article:
No other information about the fund available on American Beacon website.
More detailed information in the SEC filing. Ionic was managing the strategy since August 2013, and the performance has not been stellar: the fund returned only 3.2% since inception til end of 2014. Proposed managed fee is little over 1%. However this is not particularly surprising - afaik Ionic strategy is specifically long convexity, and would likely to underperform at times of stagnant volatility, like we had in the past few years.The American Beacon Ionic Strategic Arbitrage Fund ... [through it's] sub-advisor, Ionic Capital Management, will pursue ... a market-neutral ... strategy that consists of ...40-50% of the fund’s assets will be allocated to convertible arbitrage;20-30% will be allocated to credit/rates relative value arbitrage;30-40% will be allocated to equity arbitrage; and5-15% to volatility arbitrage.
No other information about the fund available on American Beacon website.
High / Low Timing Patterns, Part 2
Comment from reader Rich on yesterday's post prompted me to run a quick investigation - does adjusting bars helps to bring distribution of highs and lows closer to theory? The answer is definitely yes, but as everything else in life the reality is complicated. Here's what I found:
Using SPY data for 2013 and 2014, and dividing trading day into 7 equal time intervals of about 56 minutes the percentages of highs and lows (and theoretical from arcsine law) are as follows:
Using SPY data for 2013 and 2014, and dividing trading day into 7 equal time intervals of about 56 minutes the percentages of highs and lows (and theoretical from arcsine law) are as follows:
| highs | lows | theoretical |
|---|---|---|
| 30% | 42% | 25% |
| 11% | 14% | 11% |
| 9% | 8% | 10% |
| 6% | 4% | 9% |
| 7% | 7% | 10% |
| 11% | 9% | 11% |
| 27% | 16% | 25% |
So the numbers are clearly different, especially for beginning of the day, and for daily lows. However, if we divide every day into 7 buckets of equal volume, the distribution of highs and lows is actually much closer to theoretical:
| highs | lows | theoretical |
|---|---|---|
| 23% | 28% | 25% |
| 12% | 15% | 11% |
| 10% | 14% | 10% |
| 9% | 10% | 9% |
| 11% | 11% | 10% |
| 13% | 11% | 11% |
| 23% | 11% | 25% |
Both highs and lows are quite similar to what is predicted by theory. But as Rich noted in the comment, lows tend to happen more often at the start of the day than predicted by theory, even if we normalize the data by volume. This, I believe, is a legitimate pattern - although I'm not sure how to systematically capitalize on it.
High / Low Timing Patterns
Just few days ago stock.nu published a post with charts showing that empirical distribution of daily lows follows a U-shaped pattern, i.e. daily low is not equally likely to happen at any time during the trading day, rather low is more likely to occur near the open or the close. Similar (symmetric) U pattern exists for distribution of daily highs - they also more likely to happen near the open or the close.
This particular distributions of daily extremes is actually not surprising - it is one of the properties of random walk process. To re-phrase: if we were to simulate a random walk process, we would not see a uniform distribution of highs and lows throughout the day, rather we would see this U-shape pattern of highs and lows.
This phenomenon is known as arcsine law (law in this context means probability distribution) and has several manifestations. The one displayed in the charts is described in Wikipedia as Third Arcsine Law
This particular distributions of daily extremes is actually not surprising - it is one of the properties of random walk process. To re-phrase: if we were to simulate a random walk process, we would not see a uniform distribution of highs and lows throughout the day, rather we would see this U-shape pattern of highs and lows.
This phenomenon is known as arcsine law (law in this context means probability distribution) and has several manifestations. The one displayed in the charts is described in Wikipedia as Third Arcsine Law
This is theoretical distribution of lows (or highs) that we would expect according to the formula. If you compare it to the original (empirical distribution) chart, the numbers are quit similar.
However I must note that I cheated a little bit: both the empirical chart from stock.nu and mine below have seven columns, but time intervals are not the same - in the top chart the first bar corresponds to the first half-hour, while the rest are one hour. In theoretical chart all time intervals are the same.
So how much do these distributions really differ? If we recalculate the theoretical chart, we still see the U-shaped pattern, but it would look somewhat different from empirical.
What explains the differences? Well - really one thing - there is a difference in trading activity in different parts of the day. I speculate that if were to adjust the time intervals for equal trading volume, or equal number of trades, the resulting empirical distribution will be very similar.
Check out my follow-up post.
The Bubble Index: Interview with Taylor Trott
I am very pleased to introduce today Taylor Trott, author of LPPL Market Watch blog, and The Bubble Index. If acronym “LPPL” is not familiar to you, you’re about to learn about one of the most exciting subjects in mathematical finance, and that is especially important to volatility traders: quantitative prediction of market bubbles and crashes!
OnlyVIX: Taylor, tell us about yourself; what was your motivation for creating the website about market crashes?
Taylor Trott: My parents are not familiar with finance. Unfortunately, they are not alone; a big problem with the public education system in America is the lack of a good investment and finance curriculum. You can probably blame this on a number of factors, the most important of which is a lack of knowledgeable teachers because the good ones can make a much larger salary in the private industry.
As a kid, I remember my parents being frequently concerned about their finances. They lost a large amount of their savings in the internet bubble crash. They had trusted a family friend who worked in the brokerage industry. And when I was 18 in 2008 my parents again saw their entire savings disappear. Once again their money was entrusted with a friend who worked at a prominent financial investment bank. My parents may not be the smartest people, but they are some of the hardest working people you will ever meet. And it really affected me to see them lose so much of their savings.
I began to question everything I had ever read about stocks. All of the writings of Benjamin Graham and Warren Buffett represented a traditional and simple method which relied entirely on an external force - Mr. Market - to give patient investors good investments. This Mr. Market, to my curious mind needed to be elucidated. Who is Mr. Market? Why were there times when Mr. Market gave patient investors a real bargain? From a purely reductionist view, this Mr. Market is merely the sum total of all the market participants. Thus there seemed to be an answer. This question remained in my mind for a number of years.
At that time I had only recently started learning about investing. I was familiar with the strategy of Warren Buffett – “be fearful when others are greedy and greedy when others are fearful”. I thus convinced my parents to go “all in.” They put all of their money into stocks near the lows in 2009. The results since then have been well worth that decision. However, the majority of people didn't have or would not agree with my advice at that time, and ended up selling all stocks and going all into bonds at precisely the worst time!
OV: Tell us about the model that you use to monitor market bubbles and predict crashes?
TT: After graduating from college I had become fascinated by non-linear and complex systems. And when I first arrived in Boston I went straight for the library and came across a book called Why Stock Markets Crash by Didier Sornette, in which the author proposes that right before crash markets move in a specific pattern that can be described by specific mathematical function: log periodic power law (LPPL) oscillations. At the time, I remember there were some fascinating ideas being presented and the fact that the author was a physical scientist was equally appealing. It was one of the only books that I had come across which actually had made predictions of financial markets based on mathematics originating from the natural sciences. I emailed Sornette asking, quite randomly, whether similar oscillations exist in a star shortly before the supernova critical time? As you can see I was focused on anything but finance. Still, I continued for about a year to read Sornette’s book and his other papers while I had free time between my studies and college life. Eventually, we had to do a project for a class dealing with investing. So I figured I would use this as an opportunity to do some investigation into the LPPL model.
by Didier Sornette, in which the author proposes that right before crash markets move in a specific pattern that can be described by specific mathematical function: log periodic power law (LPPL) oscillations. At the time, I remember there were some fascinating ideas being presented and the fact that the author was a physical scientist was equally appealing. It was one of the only books that I had come across which actually had made predictions of financial markets based on mathematics originating from the natural sciences. I emailed Sornette asking, quite randomly, whether similar oscillations exist in a star shortly before the supernova critical time? As you can see I was focused on anything but finance. Still, I continued for about a year to read Sornette’s book and his other papers while I had free time between my studies and college life. Eventually, we had to do a project for a class dealing with investing. So I figured I would use this as an opportunity to do some investigation into the LPPL model.
I suggested to my group that we study the LPPL model and its claim to predict market crashes. They agreed and we chose this as our project. My idea was to figure out how an investor might benefit from knowing about an LPPL prediction. And to make it as simple to use as possible, so that even my parents could benefit from it. No complex equations, nothing hard. The outcome was a GIF animation created from thousands of snapshots of the DJIA. A vertical line progressed along the DJIA chart from 1893 to 2012. The screen flashed red when the code determined that an investor should exit the market because the LPPL oscillation “signal” was strong – a critical point predicting possible market crash.
That was the end of the semester and while my classmates did their summer internships, I became fascinated by the power of LPPL oscillations to really predict market crashes. To me these patterns were something bigger than just a financial predictor. They were not just occurring in financial markets but in perhaps all complex systems. Since they were first discussed in earthquake physics, I really felt that by studying these oscillations I could learn about many subjects and perhaps discover something new.
Also that summer I started reading Robert Prechter's books on Elliott Waves. How it took me so long to discover his books and ideas is surprising, especially considering I was in a Mathematical Finance program. This opened up my mind to more ideas about patterns occurring in financial markets and nature. Mankind is an emotional and social animal, despite our mass domestication and desire to lift ourselves above our human instincts. Combining Prechter's books with E. O. Wilson's sociobiology, you can see how I began to think of the collective human species as an emergent social organism. And this organism was somehow expressing certain properties of itself in the prices of market indices.
By the end of the summer I had developed an index which would monitor the power of any LPPL oscillations in real time. I was not aware of Sornette's own Alarm Index at the time, so when I found out he created a similar tool it was great news and gave me some competition. After the initial index idea, I realized it had some problems. The fundamental problem I encountered was how to determine how many days of data to include in the formula: 1 year? 3 years? 7 years? My solution was to do a set of several different lengths and compare the results to see which did the best job at predicting the major market crashes. I was encouraged by one person who found my website when it first started. He helped me figure out more about how to develop the algorithm and the website.
The original model was developed in R (programming language ) and is not complicated. It involves fitting the LPPL oscillation equation to the time series to find its coefficients; then finding how well the (H,Q) derivative of the LPPL fits a desired frequency by analyzing its spectral density (periodogram). The index does this for each day and outputs a value. This is done on a rolling basis for all possible days for which I have data.
To determine the best number of days to use in the equation was an experiment with trial and error. There were certain values, for example around 1,700 days of data, which predicted some crashes well. At the same time, it failed to predict other crashes. And those other events were actually being predicted by using a longer length of data. Something odd was occurring and it took me a long time to figure out what was happening. The more I played around with this the more I started to realize that this index is perhaps suggesting that each crash has a characteristic build-up length in time. In other words, a fractal behavior, where crashes of ANY size were occurring on ALL time scales – a scale-invariant system. And this was what Mandelbrot and Prechter had suggested in their writings on the financial markets. That reaffirmed my ideas and I continued to improve the index. I knew at this point that the only really true way to predict all crashes was to create indices for all data time lengths. In other words, a contour graph was needed.
OV: What future features / developments can we expect from your website in the future?
TT: The site will eventually contain a contour for all trade-able assets in the world. This will take some time, since I only have four computers. Also, I hope to further improve the algorithm. The algorithm currently uses a default set of parameters of the LPPL equation. However, different assets tend to have different parameters. Changes in the algorithm are important, however, they are a small part of the idea behind The Bubble Index. I like to think that I have helped to develop a structure and outlet for systemic risk monitoring which will improve the underlying economic structure of the human species.
OV: Anything else you would like to add in conclusion?
TT: One of the recent economic depressions in history occurred at a time in which we had the internet, computers, satellites, and some incredibly smart people. So why can't we solve a problem which has been around since the dawn of human civilization? How do we still have economic crashes and depressions? People suffer and starve as a result of economic disasters; sometimes entire societies can be destroyed. There are many issues and problems to solve and to me the greatest unsolved problem of capitalism is economic crashes. I hope that The Bubble Index helps to solve this problem.
One thing I would like readers to ponder: just try to visualize the immense amount of time the Earth has existed. And try to comprehend how small an instant in time the human species has existed. Now try to realize that financial crisis of 2008, the Internet Bubble, the Great Depression, and all other bubbles and crashes before those. The Bubble Index could have been created for all time lengths going back to the dawn of civilization. And we could see how bubbles have been forming and bursting for millennia. These are natural phenomena occurring in a biological social organism on the face of the planet Earth. These are fractal patterns at work. All time scales are equally important. There is no random walk - there is nothing random about the growth of far-from-equilibrium living creatures inhabiting Earth.
OnlyVIX: Taylor, tell us about yourself; what was your motivation for creating the website about market crashes?
Taylor Trott: My parents are not familiar with finance. Unfortunately, they are not alone; a big problem with the public education system in America is the lack of a good investment and finance curriculum. You can probably blame this on a number of factors, the most important of which is a lack of knowledgeable teachers because the good ones can make a much larger salary in the private industry.
As a kid, I remember my parents being frequently concerned about their finances. They lost a large amount of their savings in the internet bubble crash. They had trusted a family friend who worked in the brokerage industry. And when I was 18 in 2008 my parents again saw their entire savings disappear. Once again their money was entrusted with a friend who worked at a prominent financial investment bank. My parents may not be the smartest people, but they are some of the hardest working people you will ever meet. And it really affected me to see them lose so much of their savings.
I began to question everything I had ever read about stocks. All of the writings of Benjamin Graham and Warren Buffett represented a traditional and simple method which relied entirely on an external force - Mr. Market - to give patient investors good investments. This Mr. Market, to my curious mind needed to be elucidated. Who is Mr. Market? Why were there times when Mr. Market gave patient investors a real bargain? From a purely reductionist view, this Mr. Market is merely the sum total of all the market participants. Thus there seemed to be an answer. This question remained in my mind for a number of years.
At that time I had only recently started learning about investing. I was familiar with the strategy of Warren Buffett – “be fearful when others are greedy and greedy when others are fearful”. I thus convinced my parents to go “all in.” They put all of their money into stocks near the lows in 2009. The results since then have been well worth that decision. However, the majority of people didn't have or would not agree with my advice at that time, and ended up selling all stocks and going all into bonds at precisely the worst time!
OV: Tell us about the model that you use to monitor market bubbles and predict crashes?
TT: After graduating from college I had become fascinated by non-linear and complex systems. And when I first arrived in Boston I went straight for the library and came across a book called Why Stock Markets Crash
I suggested to my group that we study the LPPL model and its claim to predict market crashes. They agreed and we chose this as our project. My idea was to figure out how an investor might benefit from knowing about an LPPL prediction. And to make it as simple to use as possible, so that even my parents could benefit from it. No complex equations, nothing hard. The outcome was a GIF animation created from thousands of snapshots of the DJIA. A vertical line progressed along the DJIA chart from 1893 to 2012. The screen flashed red when the code determined that an investor should exit the market because the LPPL oscillation “signal” was strong – a critical point predicting possible market crash.
That was the end of the semester and while my classmates did their summer internships, I became fascinated by the power of LPPL oscillations to really predict market crashes. To me these patterns were something bigger than just a financial predictor. They were not just occurring in financial markets but in perhaps all complex systems. Since they were first discussed in earthquake physics, I really felt that by studying these oscillations I could learn about many subjects and perhaps discover something new.
Also that summer I started reading Robert Prechter's books on Elliott Waves. How it took me so long to discover his books and ideas is surprising, especially considering I was in a Mathematical Finance program. This opened up my mind to more ideas about patterns occurring in financial markets and nature. Mankind is an emotional and social animal, despite our mass domestication and desire to lift ourselves above our human instincts. Combining Prechter's books with E. O. Wilson's sociobiology, you can see how I began to think of the collective human species as an emergent social organism. And this organism was somehow expressing certain properties of itself in the prices of market indices.
By the end of the summer I had developed an index which would monitor the power of any LPPL oscillations in real time. I was not aware of Sornette's own Alarm Index at the time, so when I found out he created a similar tool it was great news and gave me some competition. After the initial index idea, I realized it had some problems. The fundamental problem I encountered was how to determine how many days of data to include in the formula: 1 year? 3 years? 7 years? My solution was to do a set of several different lengths and compare the results to see which did the best job at predicting the major market crashes. I was encouraged by one person who found my website when it first started. He helped me figure out more about how to develop the algorithm and the website.
The original model was developed in R (programming language ) and is not complicated. It involves fitting the LPPL oscillation equation to the time series to find its coefficients; then finding how well the (H,Q) derivative of the LPPL fits a desired frequency by analyzing its spectral density (periodogram). The index does this for each day and outputs a value. This is done on a rolling basis for all possible days for which I have data.
To determine the best number of days to use in the equation was an experiment with trial and error. There were certain values, for example around 1,700 days of data, which predicted some crashes well. At the same time, it failed to predict other crashes. And those other events were actually being predicted by using a longer length of data. Something odd was occurring and it took me a long time to figure out what was happening. The more I played around with this the more I started to realize that this index is perhaps suggesting that each crash has a characteristic build-up length in time. In other words, a fractal behavior, where crashes of ANY size were occurring on ALL time scales – a scale-invariant system. And this was what Mandelbrot and Prechter had suggested in their writings on the financial markets. That reaffirmed my ideas and I continued to improve the index. I knew at this point that the only really true way to predict all crashes was to create indices for all data time lengths. In other words, a contour graph was needed.
OV: What future features / developments can we expect from your website in the future?
TT: The site will eventually contain a contour for all trade-able assets in the world. This will take some time, since I only have four computers. Also, I hope to further improve the algorithm. The algorithm currently uses a default set of parameters of the LPPL equation. However, different assets tend to have different parameters. Changes in the algorithm are important, however, they are a small part of the idea behind The Bubble Index. I like to think that I have helped to develop a structure and outlet for systemic risk monitoring which will improve the underlying economic structure of the human species.
OV: Anything else you would like to add in conclusion?
TT: One of the recent economic depressions in history occurred at a time in which we had the internet, computers, satellites, and some incredibly smart people. So why can't we solve a problem which has been around since the dawn of human civilization? How do we still have economic crashes and depressions? People suffer and starve as a result of economic disasters; sometimes entire societies can be destroyed. There are many issues and problems to solve and to me the greatest unsolved problem of capitalism is economic crashes. I hope that The Bubble Index helps to solve this problem.
One thing I would like readers to ponder: just try to visualize the immense amount of time the Earth has existed. And try to comprehend how small an instant in time the human species has existed. Now try to realize that financial crisis of 2008, the Internet Bubble, the Great Depression, and all other bubbles and crashes before those. The Bubble Index could have been created for all time lengths going back to the dawn of civilization. And we could see how bubbles have been forming and bursting for millennia. These are natural phenomena occurring in a biological social organism on the face of the planet Earth. These are fractal patterns at work. All time scales are equally important. There is no random walk - there is nothing random about the growth of far-from-equilibrium living creatures inhabiting Earth.
Please visit LPPL Market Watch blog, and The Bubble Index.
Intuitive Understanding of Sornette's Formula
The formula combines log-periodic oscillations, and power-law "trend" (LPPL) - both terms will be explained below. It looks formidable on the first look, but is actually quite simple to break down into two intuitive parts.
Here's how it works: the first two terms A + B ... describe the level and trend of the price, specifically price growing at unsustainable rate ( log of price vs power of t ).
The third term C ... cos describes the oscillatory behavior of price right before crashing, and is a little more involved. We all remember regular oscillations like those created by sin or cos functions.

However these "regular waves" are not how markets behave. In order to better describe the price pattern the formula augments oscillations in such way that they increase in frequency up to the point of market crash as below ...

... and also decrease in amplitude.

Combining together trend and oscillations, the formula describes market as shown in the chart below.
Next week I will introduce Taylor Trott - author of LPPL Market Watch blog, and The Bubble Index - website specifically dedicated to tracking market bubbles in equities, currencies, and commodities worldwide.
Machine Learning in Finance Workshop
The Data Science Institute at Columbia University and Bloomberg are holding a workshop on Machine Learning in Finance. The presentations look interesting and the price is
right - just $30 if you have a valid student ID, or $100 if you don't.
Some research articles are already available for download - Shawn Mankad's research or regulatory feedback is available on his website, Marti Subrahmanyam's research on options is available here. I'm probably going; if you're looking to network send me an email.
Some research articles are already available for download - Shawn Mankad's research or regulatory feedback is available on his website, Marti Subrahmanyam's research on options is available here. I'm probably going; if you're looking to network send me an email.
Opalesque.tv Volatility Interviews
Opalesque.tv has two most interesting interviews: first, from 2012 with Michael Wexler of Maple Leaf, and second , posted earlier this month, with Dr Andrew Cumming of Blackheath Volatility Arbitrage. It is not often that you hear detailed interviews from volatility arbitrage managers, so I thought to post the links in case my readers missed it.
Volatility trading is complex, and there are many more volatility strategies than there are equity strategies, but the funds mentioned above do run a similar core strategy - both sell ATM options and buy / overbuy wings (similar strategy is purportedly traded by ex-Nassim Taleb's hedge fund). The first payout strategy is fly - which is easy to understand as short vol position; the second - short ATM longs extra wings, looks like letter W with peak at the money, and extra wings on the side. The strategy is called dragonfly, and it is much harder to provide a simple explanation. It pays off in a really calm market, loses money in a moderately volatile market, and makes money in very very volatile conditions. The payoff is obviously highly nonlinear.
Both funds are extremely diversified across all asset classes, and geographic markets. Michael Wexler notes that equities is probably the most difficult asset class for short vol, given the high level of cross-correlations at times of crisis, and competition.
Volatility trading is complex, and there are many more volatility strategies than there are equity strategies, but the funds mentioned above do run a similar core strategy - both sell ATM options and buy / overbuy wings (similar strategy is purportedly traded by ex-Nassim Taleb's hedge fund). The first payout strategy is fly - which is easy to understand as short vol position; the second - short ATM longs extra wings, looks like letter W with peak at the money, and extra wings on the side. The strategy is called dragonfly, and it is much harder to provide a simple explanation. It pays off in a really calm market, loses money in a moderately volatile market, and makes money in very very volatile conditions. The payoff is obviously highly nonlinear.
Both funds are extremely diversified across all asset classes, and geographic markets. Michael Wexler notes that equities is probably the most difficult asset class for short vol, given the high level of cross-correlations at times of crisis, and competition.
Notes From Academia: Exercise Boundary Violations in American-Style Options
Here is the link to the research paper - Exercise Boundary Violations in American-Style Options: The Rule, not the Exception
The findings are not at all surprising: options market makers do not like to provide tight quotes for ITM options, especially high-delta options, because of pick-off risk. If market makes a sudden move, HFT stock traders, or options market makers with faster infrastructure can quickly trade against a slower market maker, locking in free premium. OTM options don't move as fast, and are not as risky from this angle.
So it is only natural that bids are below the exercise boundary. Majority of option traders know as much - if only 11.5% of volume is below intrinsic value, 88.5% presumably do not make that mistake.
Abstract: An exercise boundary violation (EBV) occurs when the current bid price for an American option in the market is below intrinsic value. A seller at this price leaves money on the table and the buyer receives an arbitrage profit. In a liquid market, competition among dealers should drive up the bid prices and eliminate the arbitrage. An analysis of intraday data shows that EBVs are the norm, not the exception, with near-term in-the-money equity calls and puts the most affected. In March 2010 48.6% of all in-the-money call options had EBV bid quotes and 11.5% of trading volume in those options occurred below the intrinsic value, costing the sellers an estimated $39 million. EBVs are highly persistent throughout the day, making it rational to liquidate an option by exercise rather than selling it in the market, in sharp contrast to textbook theory. Our empirical results show early exercise is strongly related to an option's EBV.
The findings are not at all surprising: options market makers do not like to provide tight quotes for ITM options, especially high-delta options, because of pick-off risk. If market makes a sudden move, HFT stock traders, or options market makers with faster infrastructure can quickly trade against a slower market maker, locking in free premium. OTM options don't move as fast, and are not as risky from this angle.
So it is only natural that bids are below the exercise boundary. Majority of option traders know as much - if only 11.5% of volume is below intrinsic value, 88.5% presumably do not make that mistake.
Volatility of Average
Different commodity including some volatility and bitcoin futures settle to an average value. For example VSTOXX settles to 1 minute sampled average value of the index in the last half hour of trading, Bitmex XBT/USD futures settle to 1 minute sampled average value of the last two hours of trading, Atlas ATS BTC/USD futures and options settle to a 24 hour average of the last calendar day of the month.
Correct modelling of this is interesting for both options and futures pricing, as average process has obviously less volatility than "regular" process. How much less? Well, apparently I fell asleep during a class because I have no recollection of the formula until I recently researched it.
B(t) is ABM, then.gif) has variance of
has variance of.gif)
In simple terms, average has 1/sqrt(3), or about 58% of volatility.
Simple example: assume BTC/USD volatility of 100% per year. Expected volatility over 30 days should be sqrt(100 * 100 * 30/365) = 28.67%. However if the contract settles to the last day's average, for options pricing we should use volatility of sqrt(100 * 100 * 29/365 + 100 * 100 * 1/365 / 3) = 28.35%, slightly lower.
In conclusion: average settlement - interesting, but of little practical importance from pricing perspective.
P.S. Re: Atlas ATS - could not get their API to work, waiting for LedgeX.
Correct modelling of this is interesting for both options and futures pricing, as average process has obviously less volatility than "regular" process. How much less? Well, apparently I fell asleep during a class because I have no recollection of the formula until I recently researched it.
B(t) is ABM, then
.gif) has variance of
has variance of.gif)
In simple terms, average has 1/sqrt(3), or about 58% of volatility.
Simple example: assume BTC/USD volatility of 100% per year. Expected volatility over 30 days should be sqrt(100 * 100 * 30/365) = 28.67%. However if the contract settles to the last day's average, for options pricing we should use volatility of sqrt(100 * 100 * 29/365 + 100 * 100 * 1/365 / 3) = 28.35%, slightly lower.
In conclusion: average settlement - interesting, but of little practical importance from pricing perspective.
P.S. Re: Atlas ATS - could not get their API to work, waiting for LedgeX.
Updated Expiration Calendar
Happy New 2015 to volatility traders everywhere!
I have updated Expiration Calendar with expiration dates for all listed volatility futures in the world. What is new since the last update? Well, several things:
1 - Eurex added Variance Futures on Eurostoxx 50 Index (EVAR). Cannot say I'm excited about the product - CBOE tried to list variance futures twice without success.
2 - India VIX, weekly expirations on Tuesdays, 3 contracts listed at the time. Not sure who decided that NSE India needs weekly volatility contracts, instead of regular monthly contracts, like everything else on the exchange.
3 - Australia VIX, sadly the product did not attract much volume either. If I understand correctly, exchange's expiration calendar does not include expiration dates for AVIX, and I calculated them myself.
4 - Korea. After years of teasing, KRX finally listed VKOSPI futures last November. Volume is still low, but I hope that some of the KOSPI options liquidity will spill over to VKOSPI. Overall KRX seems to be on the product expansion mode. As FT reported yesterday the exchange "unveiled a 10-point plan to revive trading in Seoul, unveiling measures to relax daily price limits in its stock markets, introduce market making schemes for illiquid stocks and exempt derivatives market makers from a local transactions tax."
1 - Eurex added Variance Futures on Eurostoxx 50 Index (EVAR). Cannot say I'm excited about the product - CBOE tried to list variance futures twice without success.
2 - India VIX, weekly expirations on Tuesdays, 3 contracts listed at the time. Not sure who decided that NSE India needs weekly volatility contracts, instead of regular monthly contracts, like everything else on the exchange.
3 - Australia VIX, sadly the product did not attract much volume either. If I understand correctly, exchange's expiration calendar does not include expiration dates for AVIX, and I calculated them myself.
4 - Korea. After years of teasing, KRX finally listed VKOSPI futures last November. Volume is still low, but I hope that some of the KOSPI options liquidity will spill over to VKOSPI. Overall KRX seems to be on the product expansion mode. As FT reported yesterday the exchange "unveiled a 10-point plan to revive trading in Seoul, unveiling measures to relax daily price limits in its stock markets, introduce market making schemes for illiquid stocks and exempt derivatives market makers from a local transactions tax."
Subscribe to:
Posts (Atom)
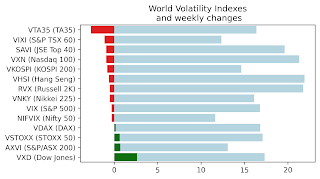
Weekly market report
Wall st delivered a mixed bag of news with VIX, VNKY, and VSTOXX and their underlying markets almost unchanged. VXD - volatility index based...
-
As I am sure all of you know Russia has began a full scale war against my home country Ukraine. Please make no mistake - Putin's goal ...
-
Another positive week for the market, and negative week for volatility. VIX and VSTOXX long term contracts continued to fall, declining by a...
-
Deutsche Bank Currency Volatility Index was developed to provide an implied volatility benchmark for major currency markets. The index is d...











