Contracts tied to volatility of Hong-Kong benchmark HSI index expired today, settling at 15.28, lower than the futures level a month ago, and closer to my forecast of 14.82. For the next expiration I forecast VHSI index to settle at 15.67 vs futures level of 17.85. It seems that the spike in VIX we experienced about two weeks ago in the was just that - a temporary specific (VHSI did not experience a parallel move) spike, and not a return to a higher volatility levels. As usual all forecasts are recorded on Forecasts Tracker spreadsheet.
Expiring Monthly
I just found out over the weekend: the editors of Expiring Monthly apparently made two back issues available for free download: July 2011 and September 2011. Enjoy!
Visual Quantitative Finance: Interview with Michael Lovelady
Q: Please tell us about your background.
A: My early educational background was in math and psychology. I think in most of what I have done since, I keep going back to those fields in some way. Starting in the late 1980s, I worked as a consulting pension actuary for Towers Watson and later for Price Waterhouse. In 1998, I started a small hedge fund with an emphasis on emerging technology. After the 2000-2002 collapse, my focus expanded to include volatility reducing strategies. In particular, blending traditional portfolio management with quantitative overlays. One of the ideas involves a hybrid options structure I call a synthetic annuity or SynA.
Q: Straight to the topic: tell us about your new book.
A: Visual Quantitative Finance
The books are related but are also meant to be standalone in scope. Profiting with Synthetic Annuities was written to propose a middle ground between modern portfolio theory and related mean-variance portfolios— which are great at capturing risk premiums over the long term but lack a risk discipline— and quantitative strategies that have great risk disciplines but are not so good at capturing risk premiums. The question is whether it is possible to bridge the gap and at what cost?
In that book, I laid out a “visual architecture” for options-based structured securities and used it to illustrate synthetic annuities structure and measure their risk/return characteristics. For the most part, the book is a practical how-to explanation for setting up options-based positions and managing them to achieve higher yields, but doing it within the constraints of risk budgets. Because I wanted to speak to institutional trustees and others who might not have a strong technical slant, I intentionally stayed away from the underlying math. So, I used a lot of graphics to communicate the ideas.
In this book, Visual Quantitative Finance
Q: Can you describe the basis of the visual method?
A: Sure, here is a figure from the book. It shows the basic framework for the visual method. It is an Excel spreadsheet with 95 Rows and seven columns. The first two columns are just a discrete approximation to the standard normal distribution. The next four columns show the stock return, the stock price, the call option payoff and the weighted call option payoff. The final column is not necessary to price the option, but it is included as a check on the drift assumption. It is a relatively straightforward way to duplicate the Black-Scholes formula without having to introduce PDEs.
Using the Black-Scholes assumptions, the spreadsheet gives a value of $11.93 compared to the actual Black-Scholes price of $11.92.
To me, the advantage of the spreadsheet is in breaking the formula into simple pieces. I like to look under the hood and see how the pieces fit together – what makes the mechanism work. In this format, it is possible to trace the assumptions through the steps of the process: stock returns, stock prices, option payoffs and weighted option payoffs. For this blog’s audience, this stuff is probably elementary, but for some people, it may help to demystify option pricing.
In this context, option pricing is a matter of adjusting the “stock return” distribution to reflect particular drift and volatility assumptions. By stepping through time or across other pricing assumptions, you can get a good idea of what is happening in the pricing mechanism. A separate figure in the book cross-references the standard stochastic stock price formulas to the spreadsheet elements.
This creates visibility into the basic components of option pricing: the option payoffs and their probabilities – in other words a random variable, where the option price is just the weighted average payoff, or the product of columns B and E.
The book expands the random variable framework to do several things. In the first part of the book, chapters 1 through 5, the visual approach is put into context compared to other pricing methods, Value-at-Risk and Conditional Value-at-Risk are explained in terms of simple lookups or slight modifications to lookups, and the formulas for the mean and standard deviation of the stock return random variable are derived that so the spreadsheet is fully functional across all Black-Scholes pricing assumptions.
In chapters 6 through 10, the random variable framework is used to present a simplified method of obtaining the lognormal distribution and then extended to a general model of options-based structured securities.
In chapters 11 through 15, the model is applied to covered calls, iron condors and synthetic annuities. There are also discussions and illustrations of analyzing option price changes and calculating greeks.
Here is a Figure from the book that illustrates the finished model for a synthetic annuity.
As another example, here is the model for a condor.
The idea behind the model is to highlight the probability curve – and how it changes over time and with different pricing assumptions – rather than obscure it inside closed-form solutions. What is surprising is how easy it is to build the model with random variables.
To make the transition between design and management, I included some material from PwSA as the last two chapters in the new book. Chapters 14 and 15 are from PwSA and talk about the practical considerations in tracking the performance of structured securities and an introduction to the design of a particular form of SynA that uses covered calls and protective puts, a form that is appropriate for more conservative investors.
Q: How can traders benefit from your book? What are the practical applications?
A: For the audience of this blog, I think there are a couple of ways. First, in managing portfolios, I think the issues around using volatility for diversification is very interesting. So far, I haven’t been able to get comfortable with any straightforward way of doing this. The first generation ETPs are very hard to use and the second generation products are still questionable in their ability to capture the right moves at low cost.
In PwSA, I devote a chapter to ideas about how a SynA might help. The chapter is called “Synthetic Annuities for the Volatility Market” and looks at an example using VXX. As I’m sure the readers of this blog know well, the challenge is to offset the high roll costs associated with holding this instrument.
The objective of a volatility-based SynA is to capture diversified returns while helping to counteract the problem of “holding” volatility. Specifically, the SynA attempts to capture the high levels of IV in short puts and short put spreads on exchange-traded instruments like the VXX. The idea is that if you can pick up theta at a rate approximately equal to the levels of negative roll yield, it can provide a useful portfolio diversifier and keep the cost of holding it down at the same time. The approach can be modified to layer in short call spreads to further counteract roll costs, especially when the level of VIX is declining, or when the shape of the curve is changing. It does require fine-tuning adjustments to improve the stability of the hedge. The same technique could be used on VXZ or other new products where options are available.
The second way, related to Visual Quantitative Finance
Visual Quantitative Finance
Subscribe to:
Posts (Atom)
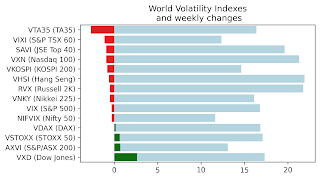
Weekly market report
Wall st delivered a mixed bag of news with VIX, VNKY, and VSTOXX and their underlying markets almost unchanged. VXD - volatility index based...
-
As I am sure all of you know Russia has began a full scale war against my home country Ukraine. Please make no mistake - Putin's goal ...
-
John “Hojun” Hwang is the author of VIX, VIX Futures, and VIX ETNs, a conceptual guide to trading the VIX index. He graduated with degrees i...
-
Wall st delivered a mixed bag of news with VIX, VNKY, and VSTOXX and their underlying markets almost unchanged. VXD - volatility index based...
